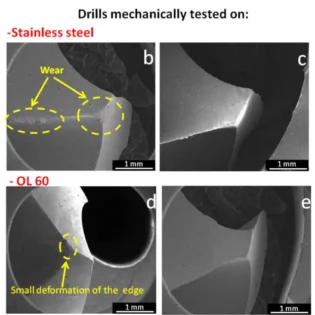
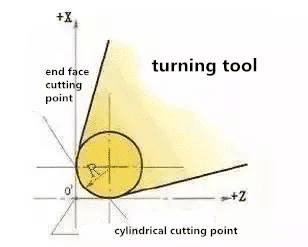
Как показано на рисунке ниже, угловой радиус образован пересеченной линией основной режущей кромкой и боковой режущей кромкой, которая также называется радиусом кромки.
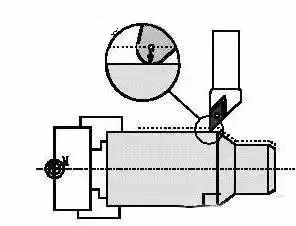
В процессе резания, чтобы повысить прочность острия инструмента и уменьшить шероховатость поверхности станка, в носовой части инструмента обычно имеется переходная дуга по окружности. Кроме того, обычное не перешлифованное лезвие имеет дугу как переход с определенным радиусом. Хотя, что касается исключительно заточенного поворотного наконечника, у него все же есть определенная арочная фаска. На любом поворотном наконечнике нет абсолютного угла.

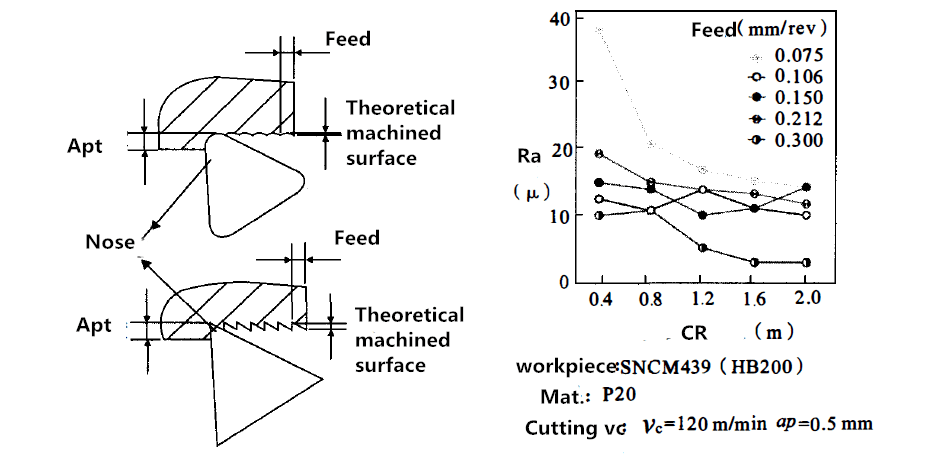
Из сравнения на рисунке 1 видно, что радиус радиуса вершины инструмента и подача на оборот оказывают наибольшее влияние на шероховатость поверхности заготовки. Для достижения теоретических требований к шероховатости поверхности, правильного радиуса вершины инструмента и скорости подачи должен быть выбран. На рисунке ниже приведена справочная таблица отношений между значениями этих трех элементов. Как правило, угловой радиус острия инструмента в три-четыре раза больше скорости подачи.
| е | Ra | |||||
| р | 0.4 | 0.8 | 1.2 | 1.6 | 2.0 | |
| 1.6 | 0.07 | 0.1 | 0.12 | 0.14 | 0.16 | |
| 3.2 | 0.1 | 0.14 | 0.18 | 0.2 | 0.23 | |
| 6.3 | 0.14 | 0.2 | 0.25 | 0.28 | 0.32 | |
| 12.5 | 0.2 | 0.28 | 0.35 | 0.4 | 0.45 | |
| 25 | 0.28 | 0.4 | 0.49 | 0.56 | 0.63 |
радиус угла r мм
f максимальная подача на рот. мм
Ра Шероховатость, мкм
Для выбора радиуса радиуса вершины инструмента и подачи на одно вращение его также можно определить с помощью теоретической эмпирической формулы (1).
Ра = Р2/ Г * 125
В которой:
Ra (мкм) – шероховатость поверхности;
f(мм/об) – подача на оборот;
r (мм) – радиус дуги вершины инструмента;
125 - постоянная.
Подставляя заданное значение радиуса радиуса вершины инструмента и величину подачи (1), мы можем вычислить теоретическую шероховатость поверхности и шероховатость поверхности.
Например: радиус дуги вершины инструмента составляет 0,8 мм, а скорость подачи
0,2 мм / г, подставляя формулу (1) в теоретическую шероховатость поверхности.
Ra = 0,22/0.8*125=6.25μm
Теоретическая шероховатость поверхности составляет: 6,25 мкм.
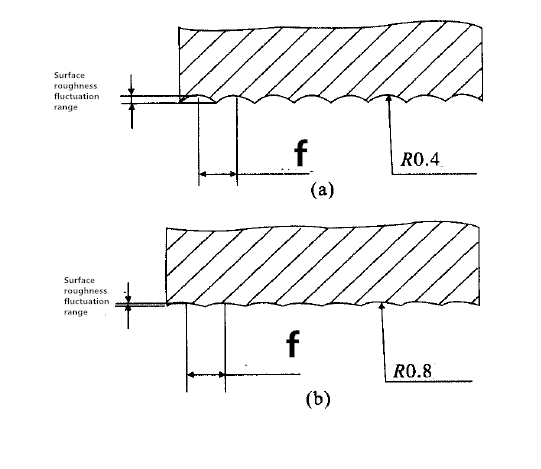
Стоит отметить, что если радиус слишком велик, вибрация будет возникать из-за чрезмерного контакта инструмента и заготовки. И наоборот, если радиус слишком мал, наконечник станет слабым и быстро изнашивается. Нужно часто резать повторно. Поэтому радиус филе обычно составляет 0,3 ~ 0,4 мм.
Компенсация радиуса коннера (радиуса кромки)
При обработке токарных станков с ЧПУ необходимо компенсировать радиус угла.
При программировании подсказка обычно рассматривается как точка, но на практике угол закруглен. Когда поверхность, такая как торец, наружный диаметр, внутренний диаметр и т.п., которая параллельна или перпендикулярна оси, обрабатывается программой, запрограммированной в соответствии с теоретической точкой наконечника, ошибки не возникает.
Тем не менее, в фактической обработке будет многократная и многократная резка. Мы обсудим следующие две ситуации:
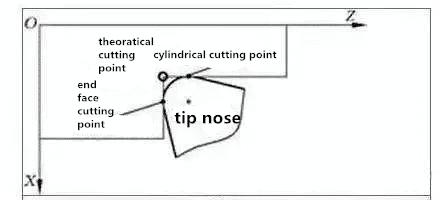
- Поворотный торец и внутренняя и внешняя цилиндрические поверхности
На рисунке ниже показан конец дуги окружности и его ориентация. Точка кончика инструмента, используемая для программирования и настройки инструмента, является идеальной точкой кончика инструмента. В связи с наличием дуги носа инструмента фактическая точка резания является точкой касания дуги края инструмента и режущей поверхности. При повороте торца фактическая точка резания дуги вершины инструмента совпадает с координатой Z идеальной точки вершины инструмента; когда используются наружное и внутреннее отверстия в машине, значение координаты X фактической точки резания и идеальной точки вершины инструмента совпадают. Следовательно, нет необходимости выполнять компенсацию радиуса вершины инструмента при повороте торца и внутренней и наружной цилиндрических поверхностей.
2) Поворот конической поверхности и поверхности дуги при обработке конической поверхности и поверхности дуги
Когда траектория обработки не параллельна оси станка, между фактической точкой резания и идеальной точкой вершины инструмента в направлениях координат X и Z имеется позиционное отклонение. Влияние радиуса вершины инструмента на точность обработки показано на рисунке ниже. Если запрограммировано с идеальной точкой наконечника инструмента, будет меньше резки или перерезания, что приведет к ошибкам обработки. Чем больше радиус дуги вершины инструмента, тем больше погрешность обработки.
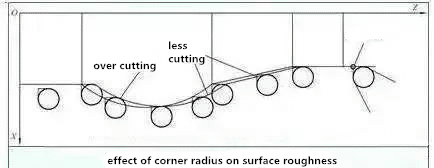
При фактической обработке токарного инструмента из-за технологического процесса или других требований острие инструмента часто является не идеальной точкой, а дугой окружности. При обработке цилиндрических и торцевых контуров, параллельных координатной оси, дуга вершины инструмента не влияет на ее размер и форму, но при обработке контуров некоординатного направления, таких как конусы и дуги, точка резания инструмента находится на дуге края инструмента. Если он изменится вверх, дуга острия инструмента приведет к ошибкам размеров и формы, что приведет к меньшему или большему количеству надрезов. Этот вид ошибки обработки, вызванный подсказкой, является не идеальной точкой, а дугой окружности, которую можно устранить с помощью функции компенсации радиуса вершины инструмента.