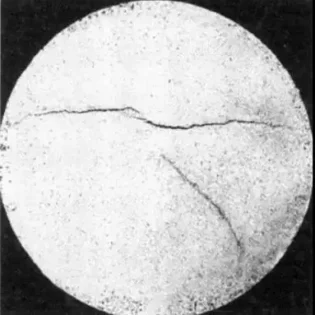
Чтобы хорошо знать модуль Юнга и ответить на этот вопрос в строке заголовка, нам нужно подумать о том, как материалы приобретают эластичность.

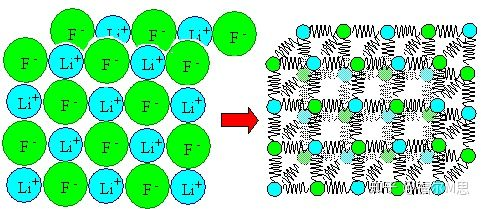
Что касается металлических материалов, мы знаем, что их внутренняя часть состоит из атомов, многие атомы расположены регулярно, образуя кристаллы, а многие зерна объединяются вместе, образуя металл, который мы обычно видим.

Возникает ли эластичность в результате взаимодействия между зернами? Очевидно, нет, поскольку эластичностью обладают и монокристаллические, и аморфные.

Таким образом, эластичность, вероятно, возникает в результате взаимодействия между атомами.

Чтобы быть максимально простым и удобным, мы стараемся не вводить сложные понятия или математические формулы. Начнем с?простейшая двухатомная модель.

Двухатомная модель модуля Юнга

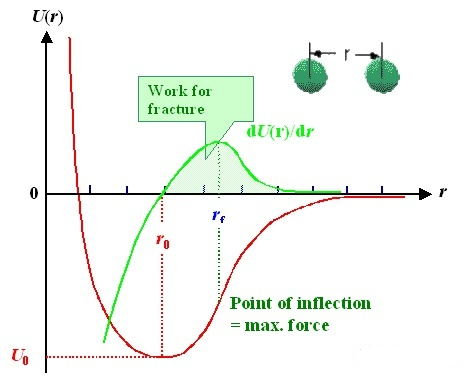
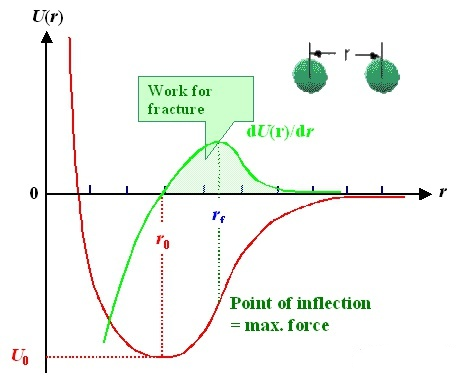
Двухатомная модель: взаимодействие между двумя атомами можно описать потенциальной функцией (красная линия). Горизонтальная ось — расстояние ?r? между двумя атомами, а вертикальная ось — потенциальная энергия U (r); Силу взаимодействия (зеленая линия) можно получить путем вывода потенциальной функции. Стоит отметить, что между двумя атомами существует положение равновесия r0r_ {0}, где сила взаимодействия F = 0 и потенциальная энергия наименьшая; Другими словами, когда вы покидаете это положение. Неважно, влево или вправо, будет сила, пытающаяся вытащить его обратно.

Подобно пружине, в естественном состоянии существует такое положение равновесия. Неважно, сжимаете ли вы пружину или растягиваете ее, она все равно возвращается в исходное положение после отпускания руки.

Это источник эластичности на атомном уровне!

Конечно, настоящие металлы или другие материалы содержат внутри много атомов. Эти атомные взаимодействия можно просто понимать как суперпозицию пары атомных взаимодействий.

анализ связи модуля Юнга с другими параметрами

В общем случае можно просто предположить, что эта потенциальная функция имеет следующий вид:

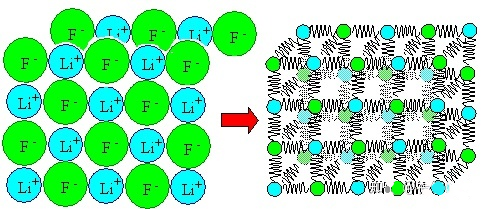
Вышеупомянутая функция имеет четыре переменных параметра, которые представляют собой положение равновесия R0R_.{0}, Энергия ожидания U0U_{0}и параметры N и M. Вышеуказанные параметры могут различаться для разных типов атомов.

Теперь мы возьмем эти два атома как независимую систему и растянем или сожмем их.

Чтобы изменить расстояние между двумя атомами вблизи положения равновесия, необходимо приложить силу F.

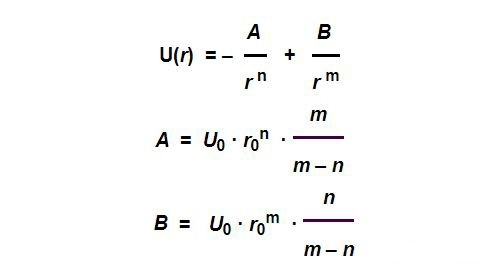
Чтобы соответствовать модулю Юнга, нам нужно изменить его на σ= E ε Form, разделить на один r02r с обеих сторон_(dá) {0} ^ {2} и подставить приведенную выше формулу и сделать вид, что работает:

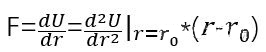
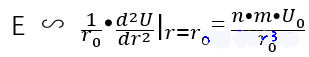
Вывод

Другими словами, на модуль Юнга E в основном влияют N, m, u0u_ {0}、r0r_ {0}. Вид атомов и температура могут влиять на эти параметры. Влияние разных видов атомов очевидно, и все параметры изменятся. Влияние температуры кажется менее очевидным.

Чтобы наблюдать влияние температуры, нам придется вернуться к самой кривой потенциальной функции. Поскольку потенциальная функция не является идеальной симметричной кривой, повышение температуры означает, что атом движется более энергично, а диапазон движений становится больше, например, тепловое расширение и холодное сжатие. В это время позиция баланса r0r_ {0} будет смещена, как показано зеленой линией на следующем рисунке.

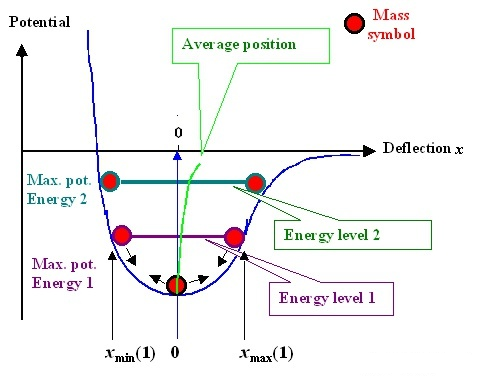
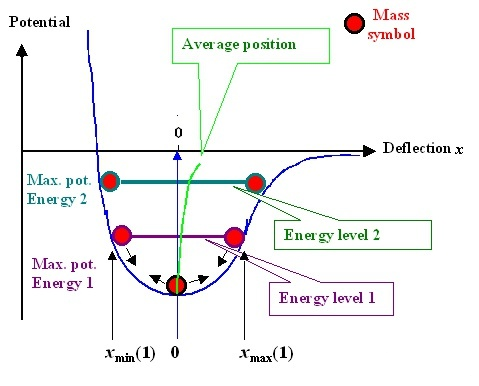
Можно доказать, что атомы всегда находятся в движении. При высокой температуре положение равновесия r0r_ Чем больше {0}, тем увеличивается объем материала и уменьшается модуль Юнга.

Возвращаясь к нашему первоначальному вопросу, количество атомов железа в разных марках стали может составлять более 901ТР3Т. Даже по сравнению с чистым железом сила взаимодействия между атомами сильно не меняется, поэтому на его модуль Юнга почти не влияет изменение состава сплава; Точно так же, независимо от изменений микроструктуры или наклепа, перестановка атомов не меняет силы между атомами, поэтому они не влияют на модуль Юнга.

Помимо модуля Юнга, из этой модели также можно вывести физические величины, такие как температура плавления, коэффициент теплового расширения и предел прочности идеального кристалла.

Что касается аномального явления, заключающегося в том, что модуль Юнга резины в высокоэластичном состоянии увеличивается с повышением температуры, то это связано с тем, что источник эластичности резины отличается от источника эластичности обычных материалов.