In recent decades, lithium-ion batteries have attracted attention in the field of energy materials. At the same time, with the development of basic theory and computer field, many computational simulation methods have been applied in the research of lithium-ion batteries. Due to errors in the experimental process, microscopic scales, such as the growth mechanism of SEI membranes, the diffusion dynamics of ions in electrode materials, the evolution of structures during charge and discharge of electrode materials, the relationship between potential and structure, and the distribution of space charge layers cannot be solved. Intuitive conclusions, experimental methods can not give a clear theoretical explanation. In contrast, computational simulation methods have relative advantages in understanding the evolution of internal chemistry and electrochemistry of lithium-ion batteries. Theoretical calculations verify the experimental results of lithium-ion battery materials, and also promote and guide the development of battery materials. Below we introduce several commonly used analog calculation methods and their applications in lithium-ion batteries.
Application of Density Functional Theory
Density functional theory has been widely used in lithium ion battery research. It is commonly used to calculate the structural stability, lithium insertion potential, electronic structure, energy band, relaxation structure, defect generation energy, migration path, activation energy and lithium. Properties such as ion transport kinetics and deintercalation of lithium phase transitions.
The voltage value of the battery is a parameter associated with a change in the free energy of the battery reaction. Different materials have an inherent lithium insertion potential. The electrode material ideally has a higher potential for the positive electrode, a lower potential for the negative electrode, and a potential difference between the different electrodes. Lithium-ion battery power can be calculated according to the battery response: (1 mol electron power is expressed by F, and an electron e? power is
1.602×10?19 C)F=NA·e?=96487.56 C/mol
Let n be the number of charges transferred during the battery reaction, then the battery through the battery is nF, the maximum electrical work done by the battery is:
?Wr’=nFVAVE
Under isothermal isostatic conditions, the Gibbs free energy of the system is equal to the work done by the system to the outside world:
ΔG=?Wr’
ΔG =nFVAVE ,And because Li+ has a unit of charge, VAVE=ΔG/F
ΔG is the Gibbs free energy of the battery reaction, assuming that the change in volume and entropy caused by the cell embedding reaction is negligible, then
ΔG≈ΔE
so:VAVE=ΔE/F
For a battery system in which the positive electrode is LiA and the negative electrode is B, it is assumed that x lithium is removed from LiA and embedded in B after charging (positive charging process), and the reaction formula is:
LiA+B→ Li1?xA+LixB
The average voltage of this process is the difference between the energy of each lithium corresponding end state (Li1?xA, LixB) and the initial state (LiA, B), then the voltage:
V=[E(Li1?xA)+ E(LixB)?E(LiA)?E(B)]/xe
When the negative electrode is metallic lithium, it can be simplified as:
V=[E(Li1?xA)+ E(Lix)?E(LiA)]/xe
By calculating the total energy of each substance before and after the reaction, the electrode potential can be calculated according to the above formula. However, for almost all cathode materials, the voltage calculated by density functional theory is low. By applying a +U correction to the standard GGA, that is, the GGA+U method, or using the hybrid functional HSE06, a voltage closer to the experimental value can be obtained. In the calculation of oxide cathode materials containing 3d transition metal ions, the strong correlation effect has been recognized as an effect to be considered.
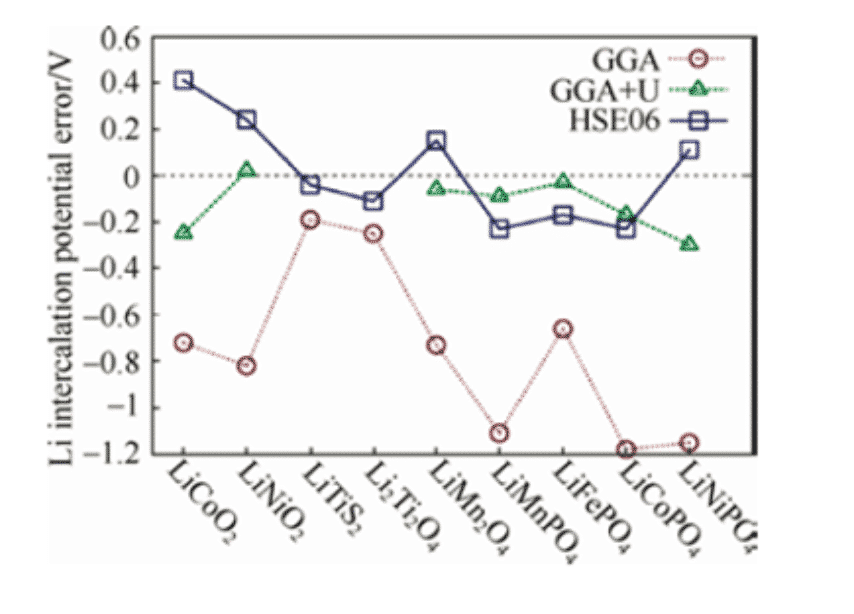
Figure 1: Standard GGA and GGA+U, HSE06 Calculate various lithium ions
Molecular dynamics method
The first-principles calculation based on density functional can obtain the properties of the material in the zero-temperature ground state. The transport of atoms and ions in the material can be studied by molecular dynamics simulation at finite temperature. Molecular dynamics calculation is used as an atomic-level simulation method using empirical potential function. Compared with the first-principles method, it can perform larger-scale simulation, which can better display the lithium ion dynamic diffusion process and analyze it.
Molecular dynamics can simulate the evolution of system particles over time, look at the path of ion migration, calculate the diffusion coefficient of particles and the stability of materials, but the law of particle motion is Newtonian mechanics, and the existence of low-quality particles such as hydrogen and helium The quantum effect calculation effect is not ideal. In terms of lithium-ion batteries, molecular dynamics can obtain the diffusion coefficient and migration path of ions in materials, which provides us with the possibility to understand the diffusion mechanism of ions in materials.
Yang calculated the self-diffusion process of LiFePO4 and found that the migration of Li+ in the material does not occur continuously, but occurs through the transition between adjacent lattice positions. In 2014, Zhang Jungan and others from Shanghai University used molecular dynamics to simulate the diffusion behavior of lithium ions between graphite layers during charging. The lithium ion diffusion properties of graphite anode materials at 300 K were studied. The experimental results provide basic data for the continuous scale model study of lithium ion battery electrode deformation.
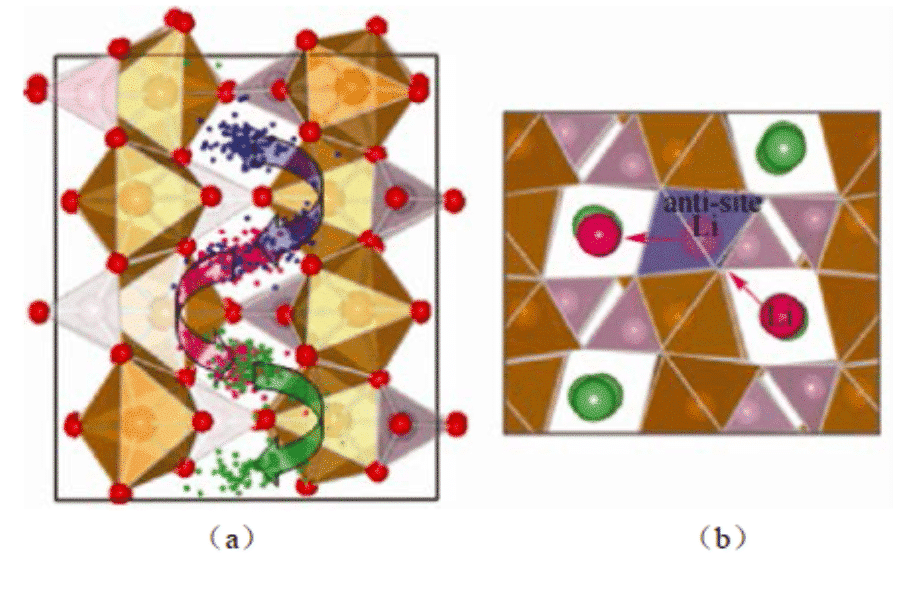
Figure 2: Molecular dynamics simulation shows (a) the trajectory of Li ions in LiFePO4; (b) the migration of Li ions between the channels through Li/Fe mutual occupation defects
Phase field model
The phase field method is based on the Ginzburg-Landau theory. The differential equation is used to represent the diffusion, ordering potential and thermodynamic drive of a specific physical mechanism. The above equations are solved by computer programming. Study the instantaneous state of the system in time and space. The phase field model is based on the fundamental principles of thermodynamics and dynamics and is a powerful tool for predicting the evolution of microstructures during solid-state phase transitions.
The phase field model can simulate crystal growth, solid phase transformation, crack evolution, film phase transition, ion migration at the interface, etc., but the simulation results are lack of quantitative comparison with time observation. The interface thickness is usually set larger than the actual situation. , leading to the lack of details. Marnix Wagemaker (Corresponding author) of Delft University of Technology in the Netherlands published an article in the journal Adv.Funct.Mater. in 2018 to propose a thermodynamic phase field model for lithium ion insertion into spinel Li4Ti5O12, integrating DFT data. The ability to describe the complete thermodynamic behavior of phase-separated particles provides a specific direction for designing the best performance Li4Ti5O12 electrode.

Figure 3: LTO single-particle simulation, the relationship between battery capacity and nominal discharge capacity and electrode thickness under porous electrode simulation
Finite element method
The finite element method is a numerical technique for solving the approximate solution of the boundary value problem of partial differential equations. The flow of the finite element method simulation is as follows: 1. Discretization of the solution problem area 2. Determine the state variable and variable control method of the region, that is, the evolution equation of the variable time space; 3. Derivate the single unit, assemble the unit The overall solution is solved, and finally the simultaneous equations are solved and the results are obtained.
In order to better understand the overheating behavior of large-capacity and high-power lithium-ion batteries for electric vehicles, Cao Binggang of Xi’an Jiaotong University used finite element method to simulate the internal temperature of the battery during consideration of internal resistance, convection and external dissipation. The spatial distribution, the temperature distribution simulation results of the test cell in a 155 °C hot furnace and the battery composition of VLP50/62/100S-Fe (3.2 V/55 A·h) LiFePO4/graphite.
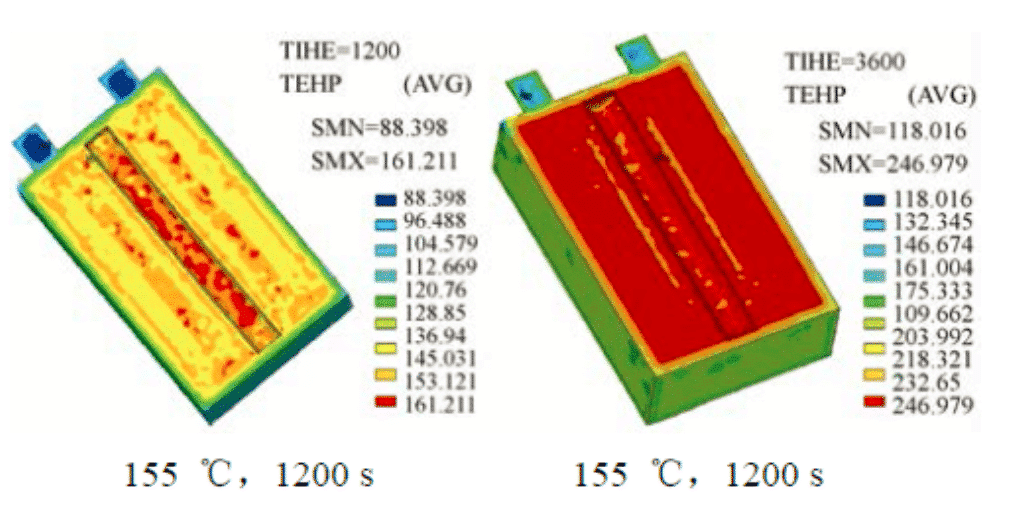
Figure 4: Distribution of finite element simulations in the cell at 155 °C, 1200 s and 3600 s
Macroscopic material simulations such as phase field models and finite element methods focus on engineering issues and help to understand macroscopic phenomena such as stress, heat transfer, flow, and multi-field coupling in lithium-ion batteries. The first-principles calculation based on density functional theory is more conducive to the microphysical properties such as energy and electronic structure of the material system.
With the development of theory and the extensive application of computer simulation, computational materials science will lead and verify experimental materials science. The calculation from macroscopic scale to microscopic theory will greatly promote the development of materials field, for lithium-ion batteries. In terms of the many problems in the experimental science, with the help of computational simulations, it will also be a clear theoretical explanation. An understanding of the computational simulation methods for lithium-ion batteries will accelerate the development and application of lithium-ion battery materials.
Reference:
[1] Huang Jie, Ling Shigang, Wang Xuelong, et al. Basic Science Problem of Lithium Ion Battery (XIV)——Computation Method[J]. Energy Storage Science and Technology, 2015, 4(2): 215-230.
[2] Ji Xiang, Song Yicheng, Zhang Jungan. Molecular Dynamics Simulation of Diffusion Properties of Li_xC_6 in Lithium Ion Batteries[J]. Journal of Shanghai University(Natural Science), 2014(1): 68-74.
[3] Shi Siqi (Sisi Qi). First-principles study of cathode materials for lithium-ion batteries [D]. Beijing: Institute of Physics Chinese Academy of Sciences, 2004. [4] Yang J J,Tse J S. Li ion diffusion mechanisms in LiFePO4:An abinitio molecular dynamics study[J]. J. Phys. Chem. A,2011,115 (45):13045-13049.
[5] Vasileiadis A, Klerk N J J D, Smith R B, et al. Toward Optimal Performance and In‐Depth Understanding of Spinel Li4Ti5O12 Electrodes through Phase Field Modeling[J]. Advanced Functional Materials, 2018.
[6] Herzmann C, Günther G, Eker B, et al. Three-dimensional thermal finite element modeling of lithium-ion battery in thermal abuse application[J]. Journal of Power Sources, 2010, 195(8):2393-2398.