Теория функционала плотности (DFT) широко используется в областях физики конденсированных сред, материаловедения, квантовой химии и наук о жизни в качестве приближенного метода для работы с многочастичными системами. Например, рисунок 1(c) представляет собой структуру сверхъячейки из 72 атомов, рассчитанную с использованием метода DFT [1]. Метод вычислительного моделирования материаловедения на основе DFT может не только изучать существующие материалы, но и предсказывать новые материалы.

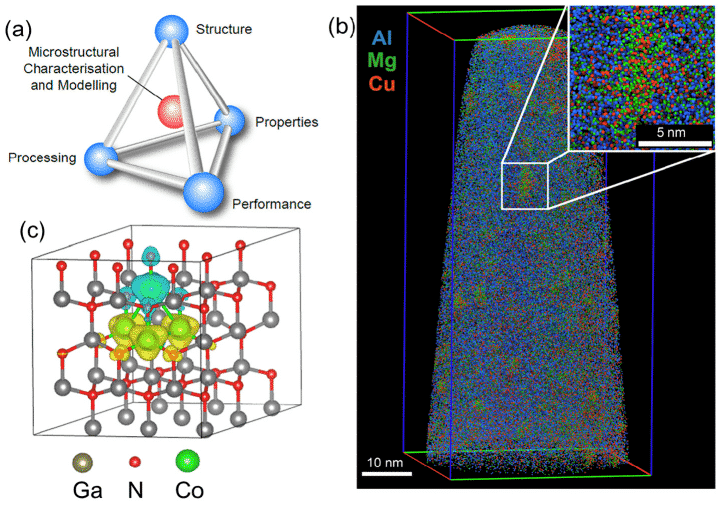
Рисунок 1 (a) Возможная связь между микроскопическими характеристиками, структурой, обработкой, свойствами и свойствами, (b) данные APT для сплавов Al-Cu-Mg, содержащих примерно 20 миллионов атомов, (c) 72 атома для расчетов DFT Пример Supercell

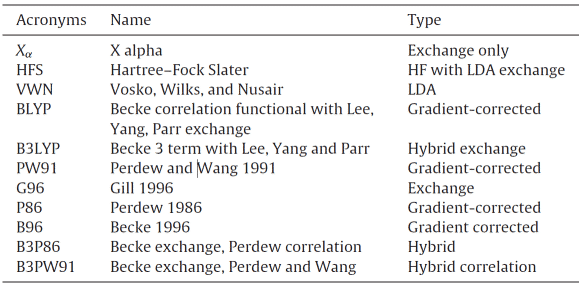
Функционал — это отображение векторного пространства в скалярное, функция от функции. В таблице 1 перечислены некоторые из предложенных типов функционалов плотности, некоторые из которых получены из базовой квантовой механики, а некоторые — из параметрических функций, каждая со своими преимуществами и недостатками и сферой применения [2]. Суть метода DFT заключается в использовании электронной плотности в качестве носителя всей информации в молекулярном (атомном) основном состоянии, а не волновой функции отдельного электрона, так что многоэлектронная система может быть преобразована в многоэлектронную систему. проблема одного электрона. Предполагая, что число электронов равно N, число переменных в волновой функции равно 3N, а теория функционала плотности сокращает число переменных до трех пространственных переменных, что упрощает процесс расчета и обеспечивает точность расчета.

Таблица 1. Некоторые приблизительные функциональные типы плотности

Развитие теории функционала плотности можно условно разделить на три этапа. Первый этап был в 1927 году. Томас и Ферми предложили модель Томаса-Ферми, основанную на гипотезе идеального электронного газа в идеальных условиях. Впервые было введено понятие теории функционала плотности, ставшее прообразом более позднего метода DFT.

Отправной точкой модели Томаса-Ферми является предположение об отсутствии взаимодействия между электронами и внешних помех, тогда уравнение Шрёдингера для движения электронов может быть выражено как:

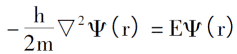
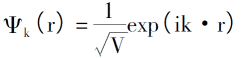
Вводя закон расположения электронов при 0K, плотность электронов, полная энергия одиночных электронов и плотность кинетической энергии системы равны:

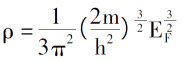
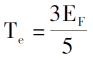
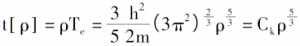
Вводя описание кулоновского потенциала и внешнего поля между электронами, можно получить выражение полной энергии электронной системы, определяемое только функцией электронной плотности [3].

Хотя модель упрощает форму и процесс расчета, она не учитывает взаимодействие между электронами. Он не точно описывает элементы кинетической энергии, поэтому он неприменим во многих системах. Однако, вдохновленные этой новой исследовательской идеей, соответствующие ученые в основном усовершенствовали содержание теории функционала плотности в 1960-х годах после многих лет усилий и, наконец, создали строгую теорию функционала плотности.

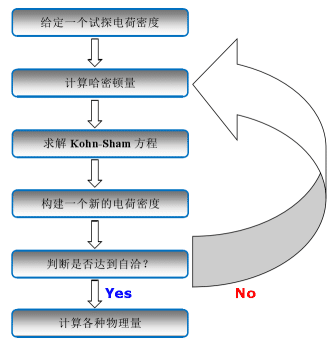
Рис. 2. Схематическая диаграмма самосогласованного итерационного процесса на основе ДПФ.

Теорема Хоэнберга-Кона и уравнение Кона-Шэма сыграли ключевую роль в формировании и улучшении метода DFT и были провозглашены двумя краеугольными камнями DFT.

(1) Теорема Хоэнберга-Кона

Основная идея теоремы Хоэнберга-Кона состоит в том, что все физические величины в системе могут быть однозначно определены переменными, содержащими только электронную плотность, а метод реализации заключается в получении основного состояния системы с помощью вариационного принципа. Эта теория в основном предназначена для модели неоднородного электронного газа и состоит из двух подтеорем. i) электронная система, не учитывающая спин при внешнем потенциале (потенциале, отличном от электронного взаимодействия), внешний потенциал которого однозначно определяется электронной плотностью; ii) для данного внешнего потенциала энергия основного состояния системы является минимумом функционального значения энергии. Таким образом, энергетический функционал системы может быть описан как:

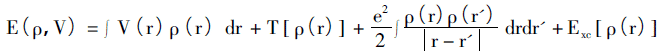
Правая часть уравнения представляет собой потенциальную энергию, член кинетической энергии, кулоновское взаимодействие между электронами и связанную с обменом потенциальную энергию во внешнем поле.

Эта теорема не дает конкретных выражений функции электронной плотности, функционала кинетической энергии и функционала, связанного с обменом, поэтому конкретное решение пока невозможно.

(2) Уравнение Кона-Шама

До 1965 г. Кон и Шэнь Луцзю установили уравнение Кона-Шама, дав подробное описание каждого пункта, и теория функционала плотности начала вступать в стадию практического применения. Они предложили для функционалов кинетической энергии использовать функционалы кинетической энергии частиц без взаимодействия для аппроксимации замещения, а различия между ними включены в неизвестные функционалов, связанных с обменом [4]. изменение Φi(r), а множитель Лагранжа заменяется на Ei. Одноэлектронное уравнение:

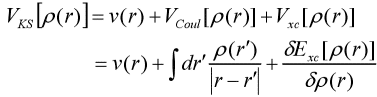
Это уравнение Кона-Шама.

Уравнение Кона-Шэма дает четкое выражение всему, что не связано с обменным функционалом, а также классифицирует сложные эффекты в этом термине. На этом этапе вычислительная сложность значительно упрощается, и вся работа начинается с описания функционального расширения, связанного с обменом. В то же время приближенный вид обменного потенциала также непосредственно определяет точность теории функционала плотности.

Метод аппроксимации локальной плотности (LDA) также был предложен Коном и Шен Луцзю в 1965 году. Цель состоит в том, чтобы аппроксимировать неизвестные ассоциации обмена, чтобы метод DFT можно было использовать для фактических расчетов. LDA использует функцию плотности однородного электронного газа для расчета отношения обмена неоднородного электронного газа. Предполагая, что плотность электронов в системе очень мало меняется с пространством, соотношение обмена неоднородного электронного газа можно выразить как:

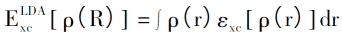
Соответствующий обменно-корреляционный потенциал может быть выражен как:

Например, Asad Mahmood et al. использовали VASP для сравнения равновесных структурных параметров расчетов LDA-PBE и GGA-PAW и изучили влияние легирования галлия на гибридизацию электронных орбит, а также оптические свойства и кристаллическую геометрию на рисунке 3 (c). Видно, что существенный вклад в проводимость вносят орбитали Ga-2s и Ga-2p, нижняя ВЗ также дает вклад Ga-2p, а примесная полоса на дне ПЗ свидетельствует о дополнительном энергетическом барьере, электрон между ВЗ и КБ. Переход должен преодолеть энергетический барьер [5].

Рис. 3. Результаты расчета

(a) Оптимизированная суперячейка ZnO 3x3x3, легированная галлием, (b) зонная структура, (c) плотность DOS

Чтобы более точно рассчитать реальную систему материалов, в 1986 г. Бекке, Пердью и Ванг и др. предложил Обобщенное приближение градиента (GGA), которое является наиболее широко используемым методом обработки при расчете функционала плотности.

Метод обработки GGA состоит в том, чтобы переписать исходное представление в функциональную форму, содержащую функции электронной плотности и градиента, а также описание спина, и результирующий функционал, связанный с обменом, выглядит следующим образом:

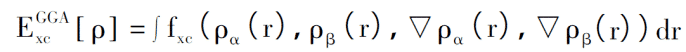
В GGA обменно-корреляционный потенциал также может быть разложен на обменную энергию и корреляционную энергию. Так как же построить разумное выражение для этих двух частей? Бекк и др. считают, что конкретная функциональная форма может быть построена произвольно в принципе и не требует учета фактического физического смысла, например, GGA-PW91; в то время как Пердью и др. выступает за максимально возможное возвращение к чистой квантово-механической теории вычислений, все физические величины только вычисляются. Начиная с основных констант, таких как электронная статическая масса, постоянная Планка и скорость света, функциональные выражения не должны содержать чрезмерных эмпирических параметров, таких как GGA-PBE (Perdew-Burke-Enzerhoff), который часто используется в таких областях, как конденсированные вещества. физика.

Недавно Parmod Kumar и L. Romaka et al. провели родственные исследования с использованием FP-LAPW (полная потенциальная линейно усиленная плоская волна) в WIEN2k и Elk v2.3.22 соответственно, в которых обменно-корреляционный потенциал представлен в виде GGA-PBE, рис. 4, 5. Результаты расчетов для соответствующих плотность состояний и распределение плотности заряда [6,7].

Рис. 4 Полная плотность состояний и локальная плотность состояний спин-поляризованных суперячеек ZnO без введения и имплантации N

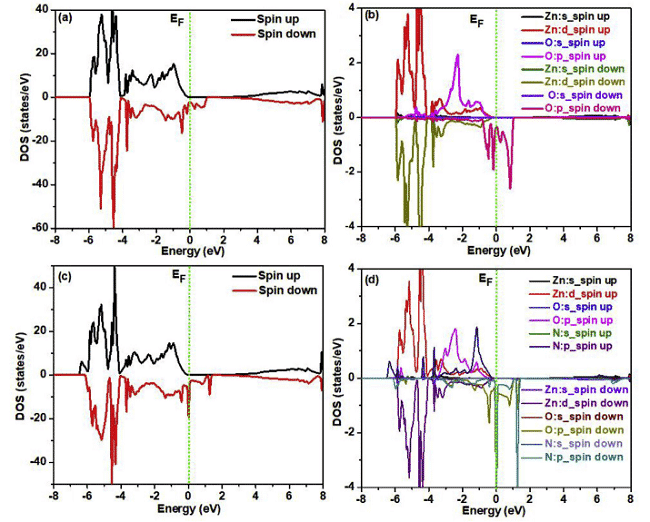
Рис. 5 Распределение функции локализации электронов (Y) и плотности заряда (r) в теллуриде VCoSb J. Ibá?ez, T. Wo?niak et al. проверил правильность различных теорий функционала плотности для предсказания динамики решетки HfS2 под давлением.

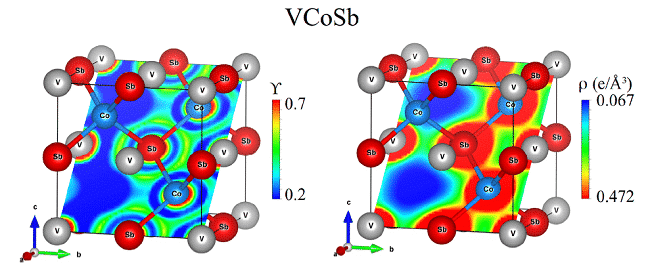
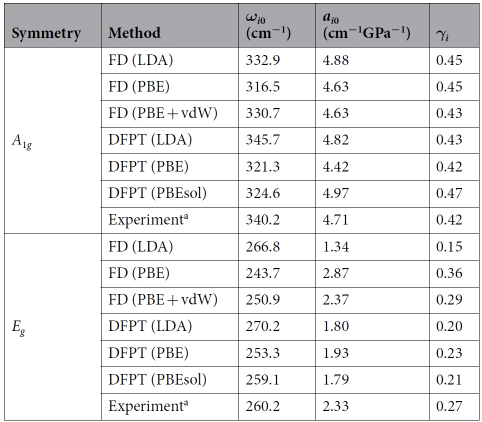
Таблица наблюдений 2 показала, что GGA-DFT правильно описывает динамику решетки HfS2 при высоком давлении с учетом взаимодействия vdW, в то время как расчет LDA-DFT широко используется для прогнозирования структуры и вибрационных характеристик 2D-соединений в условиях окружающей среды и не может быть воспроизведен при сжатии. условия. Поведение HfS2 указывает на то, что использование DFT-LDA для расчета сжимаемости TMDC и параметров Грюнайзена приведет к большим ошибкам [8].

Таблица 2. Частота комбинационного рассеяния (ωi0), коэффициент давления (ai0) и параметр Грюнайзена (γi)

В дополнение к алгоритмам LDA и GGA существуют также гибридные функционалы плотности, которые гибридным образом включают обменные эффекты Хатри-Фока (HF) в обменные ассоциации, такие как B3LYP, который был популярен в 1998 году. Эти теории содержат все больше и больше систематическая информация, и результаты расчетов становятся все ближе и ближе к экспериментальным данным, особенно подходящим для области органической химии, и достигли больших успехов в расчете механизма химической реакции.

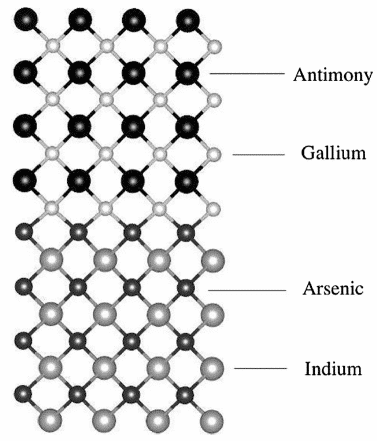
Например, Т. Гарвуд и соавт. рассчитаны данные ширины запрещенной зоны сверхрешеточной структуры типа InAs/GaSb II (модель показана на рис. 6) с использованием гибридизации типа PBE0 [9], что очень близко к экспериментальному значению, а диапазон отклонений составляет около 3 %-11%.

Рис. 6 Шарикостержневая SLS-модель InAs/GaSb гибридного DFT, рассчитанная с использованием VESTA

Теория электронной зонной структуры, основанная на одночастичном энергетическом спектре Кона-Шэма, может качественно описать многие материалы, но неудовлетворительна с количественной точки зрения. Например, для простых полупроводниковых материалов, таких как Si и GaAs, ширина запрещенной зоны, определяемая DFT Кона-Шэма при LDA / GG, намного меньше; для полупроводников с малой шириной запрещенной зоны, таких как Ge и InN, металл, полученный из LDA/GGA, является металлом. Государство, но экспериментальное наблюдение полупроводник, который является так называемой проблемой ширины запрещенной зоны LDA/GGA.

Чтобы преодолеть проблему ширины запрещенной зоны, люди приложили много усилий в теоретической основе DFT, например, расширили теорию Кона-Шама, основанную на локальном эффективном потенциале, до теории обобщенного Кона-Шама (GKS), основанной на не- локальный эффективный потенциал и другая гибридная теория функционала плотности, существует многочастичная теория возмущений, основанная на одночастичной функции Грина. В этой теории связанный с обменом потенциал с ДПФ Кона-Шэма соответствует оператору собственной энергии, связанному с обменом. Для оператора собственной энергии относительно простым и точным приближением является приближение ГВ (произведение одночастичной функции Грина G и экранированного эффекта Кулона W). Рассчитав в некотором приближении оператор собственной энергии, можно получить соответствующий ПЭС (СПС). Квазичастицы в энергии возбуждения. Хотя эти новые направления развития улучшили описание ширины запрещенной зоны материалов, приближенные функционалы по-прежнему имеют большую субъективность, а область применения относительно ограничена. Пока не существует универсального метода DFT с достаточной теоретической базой. Точное описание электронной зонной структуры материала [10,11].

Кроме того, существуют некоторые расширения, основанные на существующей теории функционала плотности. Например, теория функционала плотности, зависящая от времени (TDDFT), основанная на разности орбитальной энергии KS, используется для замены уравнения Шордингера одночастичным уравнением Дирака. Теория функционала плотности плотности распространяется на LDA+U систем с сильной корреляцией и теорию функционала плотности потока (CDFT) для работы с взаимодействующими электронными системами в произвольных магнитных полях.

Ссылки

Сян-Юань Цуй, Саймон П. Рингер，О связи между микроскопией атомного зонда и моделированием теории функционала плотности [J] ，Материалы

Характеристика (2018 г.), https://doi.org/10.1016/matchar.2018.05.015

Б. Обот, Д.Д. Макдональд, З.М. Гасем，Теория функционала плотности

(DFT) как мощный инструмент для разработки новых органических ингибиторов коррозии. Часть 1: Обзор [J]，Corrosion Science 99 (2015) 1–30

Герлингс, Ф. Де Профт, В. Лангенакер, Концептуальная теория функционала плотности, Chem. Ред. 103 (2003) 1793–1873.

Надь, Теория функционала плотности и применение к атомам и молекулам, Rev. 298 (1998) 1–79.

Кох, М.С. Холтхаузен, Руководство для химиков по теории функционала плотности, Wiley-VCH, Weinheim, 2000.

Асад Махмуд, Фатих Тезкан, Гульфеза Кардас，Термическое разложение золь-гелевого прекурсора-геля Zn0.8Ga0.2O: Акинетические, термодинамические исследования и ТФП [J]，Acta Materialia 146 (2018) 152-159

Пармод Кумар, Хитендра К. Малик, Анима Гош, Р. Тангавел, К. Асокан，Понимание происхождения ферромагнетизма в ZnO и N

имплантированные пленки ZnOthin: экспериментальный подход и подход DFT [J]，Journal of Alloys and Compounds 768 (2018) 323-328

Ромака, В.В. Ромака, Н. Мельниченко, Ю.В. Стадник, Л. Богун, А. Горынь，Экспериментальное и ТФП исследование тройной системы VeCoeSb[J]，Journal of Alloys and Compounds 739 (2018) 771-779

Ибаньес, Т. Возняк, Ф. Дибала, Р. Олива, С. Эрнандес，Р. Kudrawiec，Комбинационное рассеяние света под высоким давлением в объеме HfS2: сравнение методов теории функционала плотности в слоистых соединениях MS2 (M = Hf, Mo) при сжатии [J]，Scientific reports (2018) 8:12757，DOI: 10.1038/ s41598-018- 31051-й

Гарвуд, Н.А. Модайн, С. Кришна, Моделирование электронной структуры сверхрешеток InAs/GaSb с помощью гибридной теории функционала плотности [J], Инфракрасная физика и технологии 81 (2017) 27–31

Юджин С. Крячко, Эдуардо В. Лудена，Теория функционала плотности: обзор основ[J]，Physics Reports 544 (2014) 123–239

Б. Обот, Д. Д. Макдональд, З. М. Гасем, Теория функционала плотности (ТФП) как мощный инструмент для разработки новых органических ингибиторов коррозии. Часть 1: Обзор [J]，Corrosion Science 99 (2015) 1–30