ここ數(shù)十年、リチウムイオン電池はエネルギー材料の分野で注目を集めています。同時に、基礎(chǔ)理論とコンピュータ分野の発展に伴い、多くの計算シミュレーション手法がリチウムイオン電池の研究に適用されてきました。実験プロセスの誤差により、SEI膜の成長メカニズム、電極材料中のイオンの拡散ダイナミクス、電極材料の充放電中の構(gòu)造の進化、電位と構(gòu)造の関係、および空間電荷層の分布は解けません。直感的な結(jié)論、実験方法では明確な理論的説明を與えることはできません。対照的に、コンピューターによるシミュレーション手法は、リチウム イオン電池の內(nèi)部化學と電気化學の進化を理解する上で比較的有利です。理論計算は、リチウムイオン電池材料の実験結(jié)果を検証し、電池材料の開発を促進および指導します。以下に、一般的に使用されるいくつかのアナログ計算方法と、リチウムイオン電池でのそれらのアプリケーションを紹介します。

密度汎関數(shù)理論は、リチウム イオン電池の研究で広く使用されています。構(gòu)造安定性、リチウム挿入ポテンシャル、電子構(gòu)造、エネルギーバンド、緩和構(gòu)造、欠陥生成エネルギー、移動経路、活性化エネルギー、リチウムの計算によく使用されます。イオン輸送速度論やリチウム相転移の脫インターカレーションなどの特性。

電池の電圧値は、電池反応の自由エネルギーの変化に関連するパラメータです。異なる材料には、固有のリチウム挿入ポテンシャルがあります。電極材料は、理想的には、正電極の電位が高く、負電極の電位が低く、異なる電極間の電位差を有する。リチウム イオン バッテリの電力は、バッテリの応答に従って計算できます。

1.602×10?19 C)F=NA?e?=96487.56 C/mol

電池の反応中に転送される電荷の數(shù)をnとすると、電池を通る電池はnFであり、電池によって行われる最大の電気的仕事は次のとおりです。

?Wr'=nFVAVE

等溫等靜條件下では、システムのギブズ自由エネルギーは、システムが外界に対して行った仕事に等しくなります。

ΔG=-Wr'

ΔG =nFVAVE ，Li+ には電荷の単位があるので VAVE=ΔG/F

ΔG は電池反応のギブズ自由エネルギーであり、セル埋め込み反応による體積とエントロピーの変化が無視できると仮定すると、

ΔG≒ΔE

そう：VAVE=ΔE/F

正極が LiA で負極が B の電池システムの場合、充電後に LiA から x リチウムが除去され、B に埋め込まれていると仮定すると (正の充電プロセス)、反応式は次のようになります。

LiA+B→ Li1?xA+LixB

このプロセスの平均電圧は、対応する各リチウムの最終狀態(tài) (Li1?xA、LixB) と初期狀態(tài) (LiA、B) のエネルギーの差であり、電圧は次のようになります。

V=[E(Li1-xA)+E(LixB)-E(LiA)-E(B)]/xe

負極が金屬リチウムの場合、次のように簡略化できます。

V=[E(Li1-xA)+E(Lix)-E(LiA)]/xe

反応前後の各物質(zhì)の総エネルギーを計算することにより、電極電位は上記の式に従って計算することができます。ただし、ほとんどすべてのカソード材料では、密度汎関數(shù)理論によって計算される電圧は低くなります。通常のGGAに+U補正を加える、つまりGGA+U法、あるいはハイブリッドファンクショナルHSE06を使用することで、より実験値に近い電圧が得られます。 3d遷移金屬イオンを含む酸化物陰極材料の計算では、考慮すべき効果として強い相関効果が認められています。

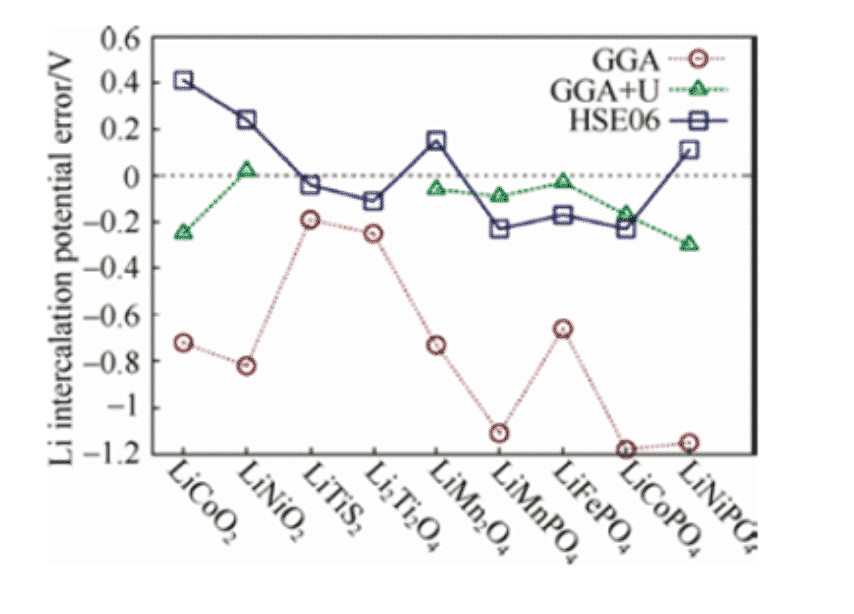
図 1: 標準 GGA および GGA+U、HSE06 各種リチウム イオンの計算

密度汎関數(shù)に基づく第一原理計算では、ゼロ溫度基底狀態(tài)での材料の特性を取得できます。材料內(nèi)の原子とイオンの輸送は、有限溫度での分子動力學シミュレーションによって調(diào)べることができます。経験的ポテンシャル関數(shù)を用いた原子レベルのシミュレーション手法として、分子動力學計算が用いられています。第一原理法と比較して、大規(guī)模なシミュレーションを?qū)g行できるため、リチウム イオンの動的拡散プロセスをより適切に表示して分析できます。

分子動力學は、時間の経過に伴うシステム粒子の進化をシミュレートし、イオン移動の経路を調(diào)べ、粒子の拡散係數(shù)と材料の安定性を計算できますが、粒子運動の法則はニュートン力學であり、低品質(zhì)の粒子の存在水素やヘリウムなどの量子効果計算効果は理想的ではありません。リチウムイオン電池に関して言えば、分子動力學は材料中のイオンの拡散係數(shù)と移動経路を求めることができ、材料中のイオンの拡散メカニズムを理解する可能性を提供します。

Yang は、LiFePO4 の自己拡散過程を計算し、材料中の Li+ の移動が連続的に発生するのではなく、隣接する格子位置間の遷移を通じて発生することを発見しました。 2014 年、上海大學の Zhang Jungan らは分子動力學を使用して、充電中のグラファイト層間のリチウム イオンの拡散挙動をシミュレートしました。 300Kにおけるグラファイトアノード材料のリチウムイオン拡散特性を研究した。実験結(jié)果は、リチウム イオン電池電極変形の連続スケール モデル研究の基本データを提供します。

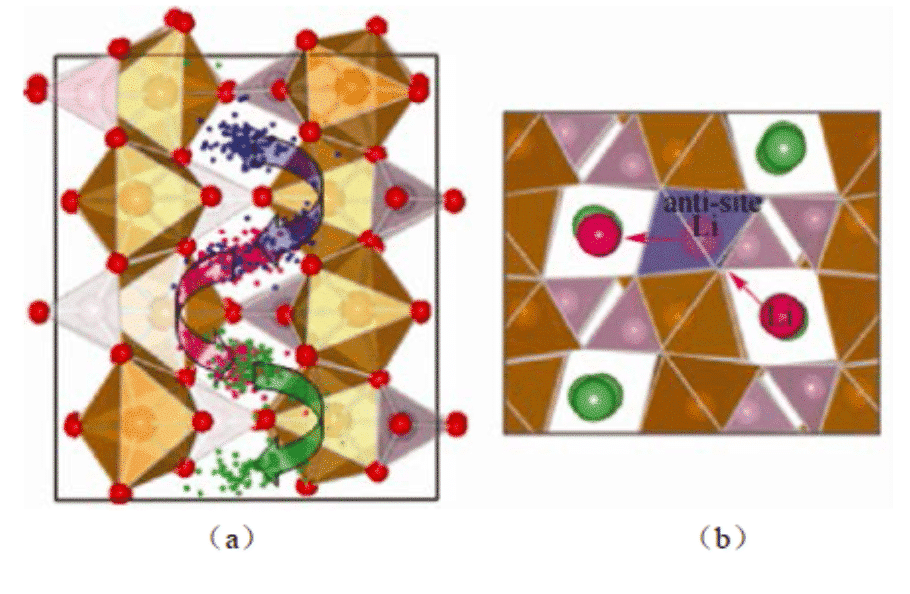
図 2: 分子動力學シミュレーションは、(a) LiFePO4 中の Li イオンの軌跡を示しています。 (b) Li/Fe 相互占有欠陥によるチャネル間の Li イオンの移動

フェーズ フィールド法は、Ginzburg-Landau 理論に基づいています。微分方程式は、特定の物理メカニズムの拡散、秩序化ポテンシャル、および熱力學的駆動を表すために使用されます。上記の方程式は、コンピュータ プログラミングによって解かれます。システムの瞬間的な狀態(tài)を時間と空間で調(diào)べます。相場モデルは、熱力學と力學の基本原理に基づいており、固體相転移中の微細構(gòu)造の進化を予測するための強力なツールです。

フェーズフィールドモデルは、結(jié)晶成長、固相変態(tài)、亀裂進展、膜相転移、界面でのイオン移動などをシミュレートできますが、シミュレーション結(jié)果は時間観測との定量的な比較に欠けています。通常、界面の厚さは実際よりも大きく設(shè)定されます。 、詳細の欠如につながります。オランダのデルフト工科大學の Marnix Wagemaker (責任著者) が Adv.Funct.Mater 誌に論文を発表しました。 2018年にDFTデータを統(tǒng)合して、スピネルLi4Ti5O12へのリチウムイオン挿入の熱力學的相場モデルを提案しました。相分離粒子の完全な熱力學的挙動を記述する能力は、最高性能の Li4Ti5O12 電極を設(shè)計するための特定の方向性を提供します。

図 3: LTO 単粒子シミュレーション、多孔質(zhì)電極シミュレーションでの電池容量と公稱放電容量および電極厚さの関係

有限要素法は、偏微分方程式の境界値問題の近似解を解くための數(shù)値手法です。有限要素法シミュレーションの流れは次のとおりです。 3. 単體の導出、ユニットの組み立て 全體解を解き、最後に連立方程式を解いて結(jié)果を得る。

電気自動車用の大容量で高出力のリチウム イオン バッテリーの過熱挙動をよりよく理解するために、西安交通大學の Cao Binggang 氏は有限要素法を使用して、內(nèi)部抵抗を考慮しながらバッテリーの內(nèi)部溫度をシミュレートしました。対流と外部散逸。 VLP50/62/100S-Fe (3.2 V/55 A·h) LiFePO4/グラファイトの電池構(gòu)成と、155 °C の加熱爐內(nèi)のテスト セルの空間分布、溫度分布シミュレーション結(jié)果。

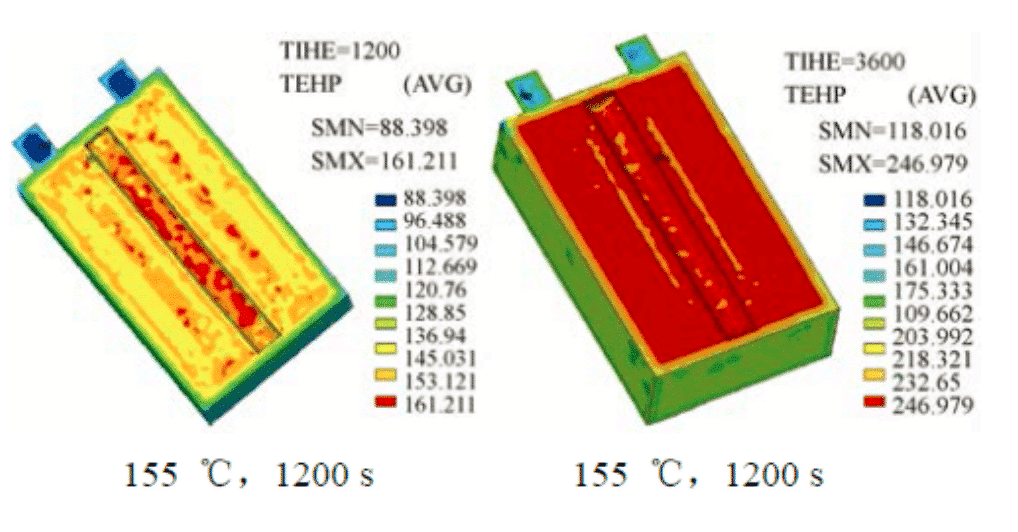
図 4: 155 °C、1200 秒および 3600 秒でのセル內(nèi)の有限要素シミュレーションの分布

フェーズ フィールド モデルや有限要素法などの巨視的な材料シミュレーションは、エンジニアリングの問題に焦點を當てており、リチウム イオン電池の応力、熱伝達、流れ、マルチフィールド結(jié)合などの巨視的な現(xiàn)象を理解するのに役立ちます。密度汎関數(shù)理論に基づく第一原理計算は、材料系のエネルギーや電子構(gòu)造などの微視的特性をより助長します。

理論の発展とコンピューターシミュレーションの広範な応用により、計算材料科學は実験材料科學をリードし、検証します。巨視的スケールから微視的理論への計算は、リチウムイオン電池の材料分野の開発を大きく促進します。実験科學の多くの問題に関して、計算シミュレーションの助けを借りて、それは明確な理論的説明にもなります。リチウムイオン電池の計算シミュレーション手法を理解することで、リチウムイオン電池材料の開発と応用が加速します。

リファレンス：

[1] 黃傑、凌世剛、王雪龍ほかリチウム イオン電池の基礎(chǔ)科學問題 (XIV) — 計算方法[J]。エネルギー貯蔵科學技術(shù)、2015 年、4(2): 215-230。

[2] ジ?シャン、ソン?イチェン、チャン?ジュンガン。リチウム イオン電池における Li_xC_6 の拡散特性の分子動力學シミュレーション [J]。上海大學ジャーナル（自然科學）、2014(1): 68-74.

[3] Shi Siqi (シシチー)。リチウム イオン電池の正極材料の第一原理研究 [D]。北京: Institute of Physics Chinese Academy of Sciences, 2004. [4] Yang JJ，Tse J S. Li FePO4 における Li イオン拡散機構(gòu)：非アビティオ分子動力學研究[J]。 Ｊ．Ｐｈｙｓ．化學。あ，2011，115（45）：13045-13049.

[5] Vasileiadis A、クラーク NJJD、スミス RB、他。フェーズ フィールド モデリングによるスピネル Li4Ti5O12 電極の最適な性能と詳細な理解に向けて [J]。先端機能材料、2018.

[6] ヘルツマン C、ギュンター G、エーカー B、他。熱亂用用途におけるリチウムイオン電池の三次元熱有限要素モデリング[J]。ジャーナル オブ パワー ソース、2010 年、195(8):2393-2398。