最初の原則は、実際には古代ギリシャの哲學(xué)者アリストテレスによって提唱された哲學(xué)用語です。各システムには、違反したり削除したりできない基本的な命題があります。各システムには、違反したり削除したりできない基本的な命題があります。

図 1 アリストテレス

物質(zhì)科學(xué)の分野では、第一原理とは原子核と電子の相互作用の原理とその基本的な運動法則を指します。量子力學(xué)を使用して、特定の要件から、一連の近似の後、シュレディンガー波動方程式を直接解いて電子構(gòu)造を取得します。これにより、システムの物理的および化學(xué)的特性が正確に取得され、微視的システムの狀態(tài)と特性が予測されます。しかし、その解決プロセスは非常に困難です。このため、ボルン＝オッペンハイマーは斷熱近似を提案しました。これは、問題全體を電子と原子核の運動と見なすことです。瞬間位置での原子核の動きを考えて、原子核の動きを考えて、電子は考えない。スペースの特定の分布。 N 電子系の場合、解決策は依然として非常に難しいため、単一電子近似が提案されています。つまり、1 つの電子のみが考慮され、他の電子は、単一の電子問題は平均場近似 [1, 2] です。

第1の原理は、斷熱近似と単一電子近似に基づく自己無撞著計算により、微小粒子の運動法則を記述するシュレディンガー方程式を解くことです。 Hartree-Fock 近似は、電子間の相互作用を無視し、電子をイオン ポテンシャル場と他の電子の平均ポテンシャル場の動きとして扱う、一種の平均場近似です。近似により、計算の精度が制限されます。 1964 年に Hohenberg と Kohn は密度汎関數(shù)理論を提案しました。この理論は、電子間の交換関連ポテンシャルを密度汎関數(shù)の形式として微妙に表現(xiàn)し、電子密度から材料の特性を決定できるようにします。それ以來、Kohn と Sham (Shen Lujiu) は、密度汎関數(shù)理論における?yún)g一電子方程式、つまり、Kohn-Sham (KS) 方程式を得て、密度汎関數(shù)理論を?qū)g際に適用させました [3, 4]。この記事では、次の側(cè)面における第一原則の最新の適用狀況を要約しています。

結(jié)晶構(gòu)造は、材料の最も基本的な特性を理解するための基礎(chǔ)であり、特に材料の微細(xì)構(gòu)造と弾性、電子、フォノン、および熱力學(xué)の固有の特性との関係を明らかにするための基礎(chǔ)です。

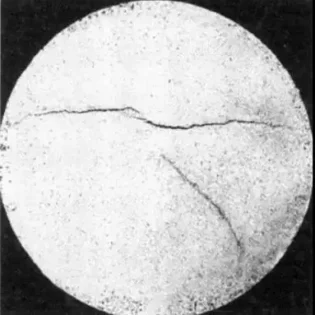
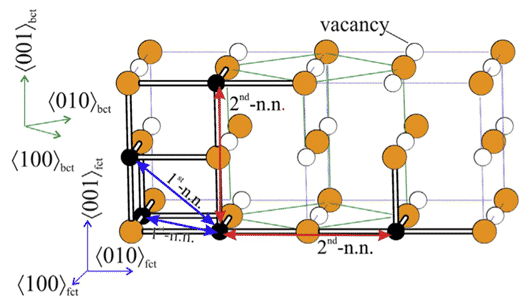
Leineweber と T. ヒッケル等。 Fe 原子の fcc 配置と構(gòu)造の一部が Bain を通過できる八面體上の N/C 原子の位置を考慮して、網(wǎng)羅的な方法を使用して、Fe4N と Fe4C の可能な構(gòu)造について DFT 計算を?qū)g行しました。歪みが安定し、図 2 に示すように、C 原子は bcc でツェナー型シーケンスを示し、格子間原子の配向傾向の特徴的な違いが明らかになり、実験的に観察されたオーステナイト構(gòu)造の違いと一致します [5 ]。

図 2 2 つの Fe 原子 (青) の fct (面心正方) 配置

超ポテンシャル平面波に基づく第一原理全エネルギー法を使用して結(jié)晶相構(gòu)造を研究し、異なる積層順序の微細(xì)構(gòu)造の熱力學(xué)的安定性を取得し、存在する可能性のある最も安定な構(gòu)造を予測します。新しいデザインと開発になります。材料の重要な手段。

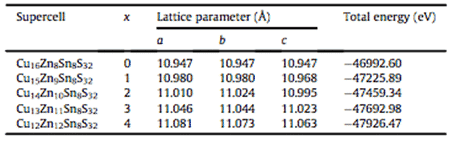
たとえば、Zhilin Li、Chunyang Xia et al。一般化勾配近似 (GGA) の下で PBE を使用して、密度汎関數(shù)理論 (DFT) に基づいて、薄膜太陽電池吸収層材料である Cu2ZnSnS4 の相安定性に関する第一原理研究を?qū)g施しました。 Cu‐Zn‐Sn‐S合金系の格子パラメータと全エネルギーを交換相関ポテンシャルにより計算し,Cu‐Zn‐Sn‐S合金における可能な相の計算モデルと生成エネルギーを確立した。結(jié)果を図 3 と表 1 に示します。示されているように、この研究は薄膜複合太陽電池用の Cu-Zn-Sn-S 合金の設(shè)計の指針となります。モデルと計算方法は、他の合金系の相安定性予測にも拡張できます [6]。

図3 64個のZnCu置換欠陥の超格子構(gòu)造モデル

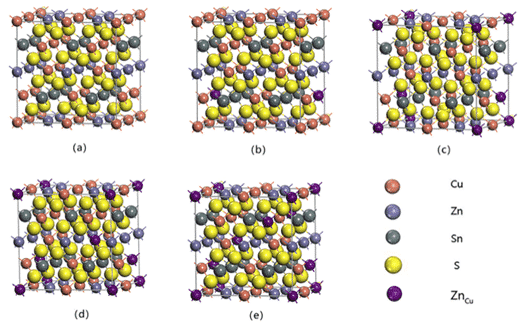
表 1 最適化された超格子構(gòu)造と全エネルギーの計算結(jié)果

安定な構(gòu)造を得るために、材料の価電子密度分布を計算することは、原子間の結(jié)合とイオン化の程度を理解する上で重要です。

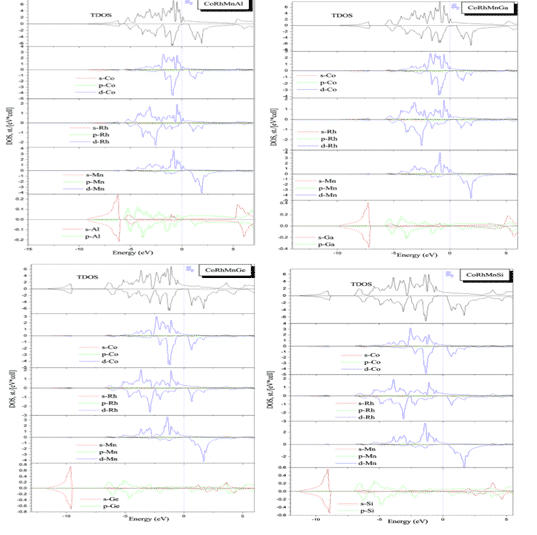
Benkabou と H. Rached ら。第 1 原理を使用して第 4 級 CoRhMnZ (Z = Al、Ga、Ge および Si) を計算グループ III、IV、または V 元素であり、一般に非強磁性元素を含みますが、化合物は強磁性を示します) 電子構(gòu)造は、全電位線形付加平面波法 (FLAPW) および GGA-PBE 近似を使用して計算されます。図4は、対応する構(gòu)造の狀態(tài)密度計算の結(jié)果を示しており、これらの化合物がいくつかの狀態(tài)、CoRhMnGeおよびCoRhMnSi化合物で半金屬強磁性體を示し、それらの磁気モーメントは基本的にスレーター?ポーリングの法則と一致しており、それらの半金屬性を示していますプロパティ。高スピン偏極、CoRhMnSi に加えて、これらの化合物は YI 構(gòu)造で安定しています [7]。

図 3 CoRhMnZ (Z = Al、Ga、Ge、Si) 安定構(gòu)造の総密度と局所狀態(tài)密度

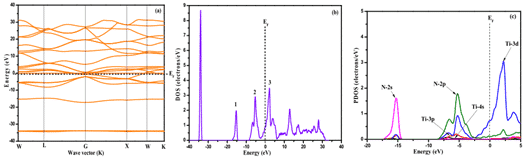
歌ら。は、最初の原理を使用して、TiN 膜の電子構(gòu)造を研究しました。図 4 に示すように、帯域は Studio Studio (MS) プログラムによってシミュレートされ、全狀態(tài)密度 (DOS)、誘電関數(shù)、および吸収が計算されました。そして反射率。

結(jié)果は、フェルミエネルギー (EF) がエネルギー準(zhǔn)位分布が密なエネルギーバンドを通過し、全狀態(tài)密度が EF と交差することを示しており、Ti-3d 狀態(tài)の電子特性によって TiN がメタロイド特性を持つことが決定されることを示しています [8 ]。

図4 TiN膜のエネルギーバンド構(gòu)造(a)、完全密度(b)、局所密度(c)

弾性定數(shù) Cij は、材料の機械的特性を表す基本的なパラメーターです。これは、原子間結(jié)合、狀態(tài)方程式、フォノン スペクトルなどの基本的な固體現(xiàn)象、および比熱、熱膨張、デバイ溫度、グリューナイゼン パラメーターなどの熱力學(xué)的特性と密接に関連しています。関連している。理論的には、21 の獨立した弾性定數(shù) Cij がありますが、立方晶の対稱性により、この値は 3 つ (C11、C12、および C44) に減少し、せん斷弾性率 G、ヤング率 E、およびポアソンは弾性定數(shù)から導(dǎo)出されます。比率 n から、平均音速 Vm からデバイ溫度を推定します。

ここで、H はプランク定數(shù)、KB はボルツマン定數(shù)、Va は原子體積、Vm はナビエの式でせん斷弾性率 G と體積弾性率 B から求められる縦方向と橫方向の音速 vl と vt によって求めることができます。 .

たとえば、Shuo Huang et al。最初の原理を組み合わせて、[001]方向のFeCrCoMnAlx（0.6≤≤1.5）高エントロピー合金體心立方固溶體相の弾性パラメーターと理想的な引張強度を決定しました。結(jié)果を図5に示します?？紤]した組成範(fàn)囲內(nèi)で、bcc構(gòu)造は、fccおよびhcp構(gòu)造の強磁性および常磁性狀態(tài)よりも低いエネルギーを持つことがわかりました。理論的なキュリー溫度に基づいて、すべての合金は室溫で強磁性であると予想され、[001] 方向の理想的な引張強度は、約 9% の最大歪みで 7.7 GPa であると予想されます。 Ａｌ濃度を下げることにより、さらに強度を上げることができる。 [9]。

Fig.5 FeCrCoMnAlx ハイエントロピー合金の弾性定數(shù)、デバイ溫度、応力-ひずみ曲線

最近、Yu Luら。は、Sn9Zn-1Al2O3-xCu 複合ろう材を使用して 6061 アルミニウム合金をろう付けし、ろう付け性能に及ぼす Cu 元素と Al2O3 粒子の添加の影響を研究しました。密度汎関數(shù)理論 (DFT) と GGA-PBE の理論に基づいて、Al2O3/Sn9Zn の界面構(gòu)造、界面エネルギー、接觸角、および電子特性に関する第一原理計算を?qū)g行しました。計算は、Sn9Zn-1Al2O3-4.5Cu と Sn9Zn-1Al2O3-6Cu が安定した構(gòu)造を持つことを示し、対応する結(jié)果を図 6 と図 7 に示します [10]。

図 6. 構(gòu)造ごとに異なる電荷密度の違いを持つ等高面:（a）Sn9Zn-1Al2O3、（b）Sn9Zn-1Al2O3-4.5Cu

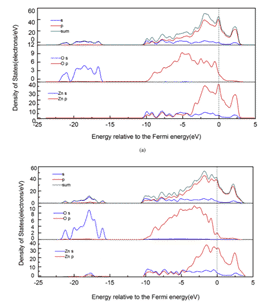
図7 異なる構(gòu)造の局在狀態(tài)密度：（a）Sn9Zn-1Al2O3、（b）Sn9Zn-1Al2O3-4.5Cu

たとえば、Kulwinder Kaur ら。密度汎関數(shù)理論 (DFT) とボルツマン透過理論を使用して、fcc HfRhSb の高溫?zé)犭娞匦预蜓芯郡筏蓼筏俊?8 と 9 は、計算されたエネルギー バンド構(gòu)造と狀態(tài)密度、およびいくつかの物理パラメータを示しています。伝送特性の理論は、バンド構(gòu)造の計算、剛體バンドにおけるボルツマン伝送理論、および定數(shù)緩和時間近似 (RTA) から始まります。リジッド パフォーマンス バンド近似 (RBA) は、バンド構(gòu)造と熱電応答の関係を調(diào)べる効果的なツールです [11]。

図 8 (a) エネルギー バンド構(gòu)造 (b) 完全な局所狀態(tài)密度 (c) フォノン分散 (d) フォノン DOS

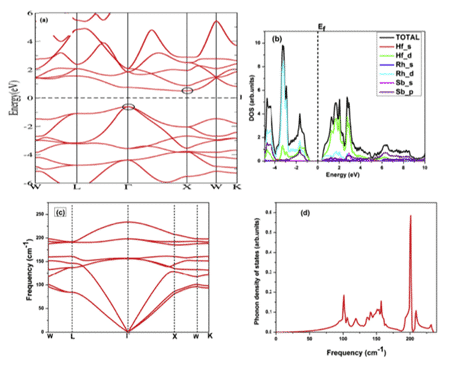
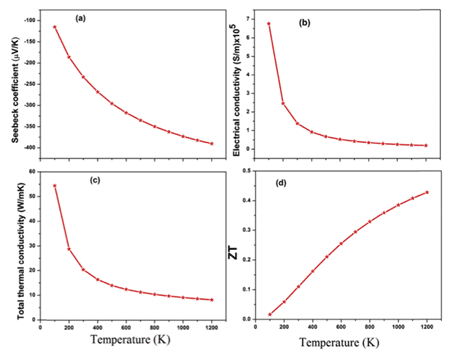
図 9 溫度の関數(shù)としてのゼーベック係數(shù)、伝導(dǎo)率、熱伝導(dǎo)率、および熱電効率 ZT

1.Heisenberg W. 運動學(xué)的および機械的関係の量子論的再解釈 [J]。 Z 物理學(xué)、1925 年、33: 879

2. Schrodinger E, Quantisierung als eigenwertproblem I [J]. Ann der Phys, 1926, 9: 361

3.Hohenberg P、Kohn W.不均一電子ガス[J]。 Phys Rev B、1964、136(3): 864

4.Kohn W、Sham L J. 交換効果と相関効果を含む自己矛盾のない方程式 [J]。 Phys Rev A、1965、140(4): 1133

5.Leineweber、T. Hickel、B. Azimi-Manavi、SB Maisel、DFT 計算によって分析された Fe4C 対 Fe4N の結(jié)晶構(gòu)造: Fcc ベースの格子間超構(gòu)造の探索 [J]、Acta Materialia 140 (2017) 433-442

6. Zhilin Li, Chunyang Xia, Zhengping Zhang, Meiling Dou, Jing Ji, Ye Song, Jingjun Liu, Feng Wang，化學(xué)量論組成から外れた薄膜太陽電池用のケステライト Cu2ZnSnS4 の相安定性に関する第一原理研究 [J]， Journal of Alloys and Compounds 768 (2018) 644-651

7.Benkabou、H. Rached、A. Abdellaoui、D. Rached、R. Khenata、MH Elahmar、B. Abidri、N. Benkhettou、S. Bin-Omran、ホイスラー四元合金 CoRhMnZ (Z= Al、Ga、Ge、Si) を第一原理計算 [J]、Journal of Alloys and Compounds 647 (2015) 276-286

8. Huijin Song, Peng Gu, Xinghua Zhu, Qiang Yan, Dingyu Yang，第一原理に基づく TiN 膜の電子構(gòu)造と光學(xué)特性に関する研究 [J]，Physica B: Condensed Matter 545 (2018) 197–202

9.Shuo Huang、Xiaoqing Li、He Huang、Erik Holmstrom、Levente Vitos、FeCrCoMnAlx high-entropy Alloys from first-principle [J]、Materials Chemistry and Physics 210 (2018) 37-42

10.Yu Lu、Le Ma、Shu-yong Li、Wei Zuo、Zhi-qiang Ji、Min Ding、Sn9Zn-1Al2O3 はんだ付け 6061 アルミニウム合金の界面挙動と機械的特性に対する Cu 元素添加の影響: 第一原理計算と実験研究 [J]，Journal of Alloys and Compounds 765 (2018) 128-139

11.Kulwinder Kaur、Ranjan Kumar、DP Rai、高溫での HfRhSb ハーフホイスラー化合物の有望な熱電応答: 最初の原理研究 [J]、Journal of Alloys and Compounds 763 (2018) 1018-1023