La théorie fonctionnelle de la densité (DFT) a été largement utilisée dans les domaines de la physique de la matière condensée, de la science des matériaux, de la chimie quantique et des sciences de la vie comme méthode d'approximation pour traiter les systèmes multiparticules. Par exemple, la figure 1 (c) est une structure de supercellule à 72 atomes calculée à l'aide de la méthode DFT [1]. La méthode de simulation informatique basée sur la science des matériaux DFT peut non seulement étudier les matériaux existants, mais également prédire de nouveaux matériaux.

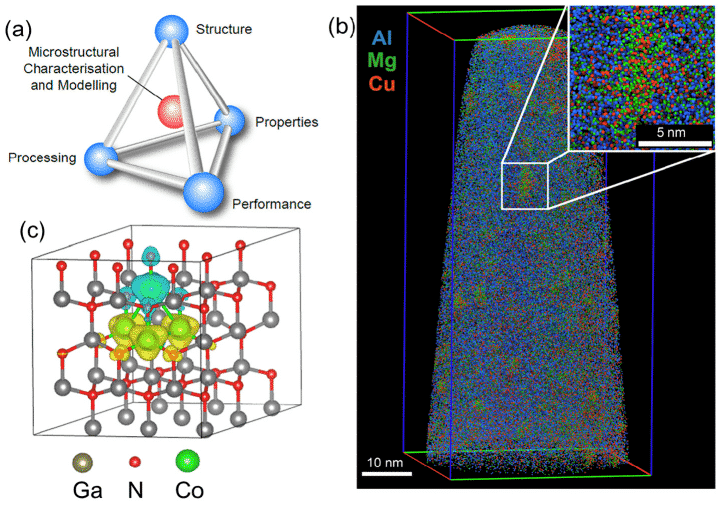
figure 1 (a) Lien potentiel entre la caractérisation microscopique, la structure, le traitement, les propriétés et les propriétés, (b) Données APT pour les alliages Al-Cu-Mg contenant environ 20 millions d'atomes, (c) 72 atomes pour les calculs DFT Exemple de supercellule

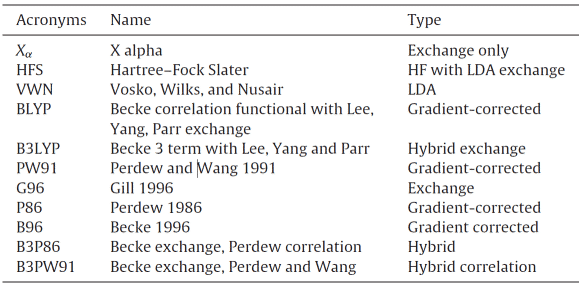
Une fonctionnelle est une application de l'espace vectoriel au scalaire, une fonction d'une fonction. Le tableau 1 répertorie certains des types de fonctionnelles de densité qui ont été proposées, dont certaines sont dérivées de la mécanique quantique de base et d'autres qui sont dérivées de fonctions paramétriques, chacune avec ses propres avantages et inconvénients et son champ d'application [2]. L'essence de la méthode DFT est d'utiliser la densité électronique comme support de toutes les informations dans l'état fondamental moléculaire (atomique), plut?t que la fonction d'onde d'un seul électron, de sorte que le système multi-électron puisse être transformé en un problème à un seul électron. En supposant que le nombre d'électrons est N, le nombre de variables dans la fonction d'onde est 3N et la théorie de la fonctionnelle de la densité réduit le nombre de variables à trois variables spatiales, ce qui simplifie le processus de calcul et garantit la précision du calcul.

Tableau 1 Quelques types fonctionnels de densité approximative

Le développement de la théorie de la fonctionnelle de la densité peut être grossièrement divisé en trois étapes. La première étape eut lieu en 1927. Thomas et Fermi proposèrent le modèle Thomas-Fermi basé sur l'hypothèse du gaz électronique idéal dans des conditions idéales. Pour la première fois, le concept de théorie fonctionnelle de la densité a été introduit, qui est devenu le prototype de la méthode DFT ultérieure.

Le point de départ du modèle Thomas-Fermi est de supposer qu'il n'y a pas d'interaction entre les électrons et pas d'interférence externe, alors l'équation de Schr?dinger pour le mouvement des électrons peut être exprimée comme suit?:

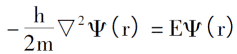
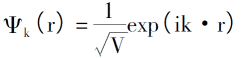
En introduisant la loi de l'arrangement électronique sous 0K, la densité électronique, l'énergie totale des électrons uniques et la densité d'énergie cinétique du système sont?:

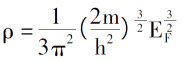
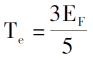
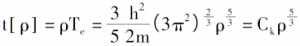
En introduisant une description du potentiel de coulomb et du champ externe entre les électrons, l'expression d'énergie totale du système électronique déterminée uniquement par la fonction de densité d'électrons peut être dérivée [3].

Bien que le modèle simplifie la forme et le processus de calcul, il ne tient pas compte de l'interaction entre les électrons. Il ne décrit pas avec précision les éléments d'énergie cinétique, il n'est donc pas applicable dans de nombreux systèmes. Cependant, inspirés par cette nouvelle idée de recherche, les chercheurs concernés ont essentiellement perfectionné le contenu de la théorie fonctionnelle de la densité dans les années 1960 après de nombreuses années d'efforts, et ont finalement établi une théorie fonctionnelle de la densité stricte.

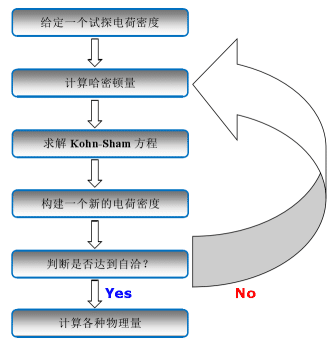
Figure 2 Diagramme schématique d'un processus itératif auto-cohérent basé sur DFT

Le théorème de Hohenberg-Kohn et l'équation de Kohn-Sham ont joué un r?le clé dans la formation et l'amélioration de la méthode DFT, et ont été salués comme les deux pierres angulaires de la DFT.

(1) Théorème de Hohenberg-Kohn

L'idée centrale du théorème de Hohenberg-Kohn est que toutes les quantités physiques du système peuvent être déterminées de manière unique par des variables contenant uniquement la densité électronique, et la méthode de mise en ?uvre consiste à obtenir l'état fondamental du système via le principe variationnel. Cette théorie concerne principalement le modèle de gaz d'électrons non uniforme et se compose de deux sous-théorèmes. i) un système électronique qui ignore le spin au potentiel externe (potentiel autre que l'interaction électronique) dont le potentiel externe peut être déterminé uniquement par la densité électronique?; ii) pour un potentiel externe donné, l'énergie de l'état fondamental du système est le minimum de la valeur fonctionnelle de l'énergie. Ainsi, la fonctionnelle énergétique du système peut être décrite comme suit :

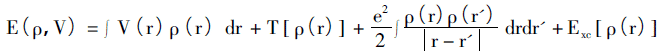
Le c?té droit de l'équation est l'énergie potentielle, le terme d'énergie cinétique, l'interaction coulombienne entre les électrons et l'énergie potentielle liée à l'échange dans le champ externe.

Ce théorème ne donne pas d'expressions spécifiques de la fonction de densité électronique, de la fonctionnelle de l'énergie cinétique et de la fonctionnelle liée à l'échange, de sorte que la solution spécifique n'est toujours pas possible.

(2) équation de Kohn-Sham

Jusqu'en 1965, Kohn et Shen Lujiu ont établi l'équation de Kohn-Sham, donnant une description détaillée de chaque élément, et la théorie de la fonctionnelle de la densité a commencé à entrer dans la phase d'application pratique. Ils ont proposé pour les fonctionnelles d'énergie cinétique d'utiliser les fonctionnelles d'énergie cinétique des particules sans interaction pour approximer la substitution, et les différences entre les deux sont incluses dans les inconnues des fonctionnelles liées à l'échange [4]. La variation de ρ est remplacée par la variation de Φi(r), et le multiplicateur de Lagrange est remplacé par Ei. L'équation à un seul électron est :

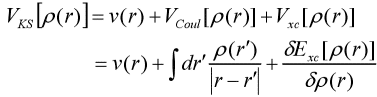
Ce qui précède est l'équation de Kohn-Sham.

L'équation de Kohn-Sham donne une expression claire à tout ce qui se trouve en dehors de la fonctionnelle associée à l'échange et catégorise également les effets complexes dans ce terme. à ce stade, la difficulté de calcul est grandement simplifiée et tout le travail commence autour de la description de l'expansion fonctionnelle liée à l'échange. Dans le même temps, la forme approximative du potentiel lié à l'échange détermine également directement la précision de la théorie de la fonctionnelle de la densité.

La méthode d'approximation de la densité locale (LDA) a également été proposée par Kohn et Shen Lujiu en 1965. Le but est d'approximer les associations d'échange inconnues, de sorte que la méthode DFT puisse être utilisée pour le calcul réel. LDA utilise la fonction de densité du gaz d'électrons uniforme pour calculer la relation d'échange du gaz d'électrons non uniforme. En supposant que la densité d'électrons dans le système change très peu avec l'espace, la relation d'échange du gaz d'électrons non uniforme peut être exprimée comme suit?:

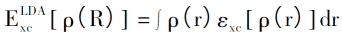
Le potentiel de corrélation d'échange correspondant peut être exprimé comme suit?:

Par exemple, Asad Mahmood et al. utilisé VASP pour comparer les paramètres structurels d'équilibre des calculs LDA-PBE et GGA-PAW, et étudié les effets du dopage Ga sur l'hybridation orbitale électronique, ainsi que les propriétés optiques et la géométrie cristalline, à partir de la figure 3 (c). On peut voir que les orbitales Ga-2s et Ga-2p contribuent de manière significative à la conduction, le VB inférieur contribue également par Ga-2p, et la bande d'impureté au bas du CB suggère une barrière d'énergie supplémentaire, l'électron entre VB et CB. La transition doit franchir la barrière énergétique [5].

Figure 3 Résultats des calculs

(a) Supercellule ZnO optimisée 3x3x3 dopée au Ga, (b) structure de bande, (c) densité DOS

Afin de calculer le système matériel réel avec plus de précision, en 1986, Becke, Perdew et Wang et al. proposé l'approximation généralisée du gradient (GGA), qui est la méthode de traitement la plus largement utilisée dans le calcul de la fonctionnelle de la densité.

La méthode de traitement GGA consiste à réécrire la représentation originale dans une forme fonctionnelle contenant des fonctions de densité électronique et de gradient, ainsi qu'une description du spin, et la fonctionnelle liée à l'échange résultante est la suivante?:

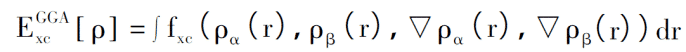
Dans GGA, le potentiel de corrélation d'échange peut également être désassemblé en énergie d'échange et en énergie de corrélation. Alors, comment construisez-vous une expression raisonnable pour ces deux parties?? Beckc et al. croient que la forme fonctionnelle concrète peut être construite arbitrairement en principe, et n'a pas besoin de considérer la signification physique réelle, telle que GGA-PW91?; tandis que Perdew et al. préconise de revenir autant que possible à la pure théorie du calcul mécanique quantique, toutes les grandeurs physiques sont uniquement calculées. à partir de constantes de base telles que la masse statique électronique, la constante de Planck et la vitesse de la lumière, les expressions fonctionnelles ne doivent pas contenir de paramètres empiriques excessifs, tels que GGA-PBE (Perdew-Burke-Enzerhoff), qui est souvent utilisé dans des domaines tels que la matière condensée la physique.

Récemment, Parmod Kumar et L. Romaka et al. effectué des recherches connexes à l'aide de FP-LAPW (onde plane améliorée linéairement à plein potentiel) dans WIEN2k et Elk v2.3.22, respectivement, dans lesquelles le potentiel de corrélation d'échange est sous la forme de GGA-PBE, Figure 4, 5 Résultats calculés pour le correspondant densité d'états et distribution de densité de charge [6,7].

Fig. 4 Densité totale d'états et densité locale d'états de supercellules ZnO polarisées en spin sans injection ni implantation de N

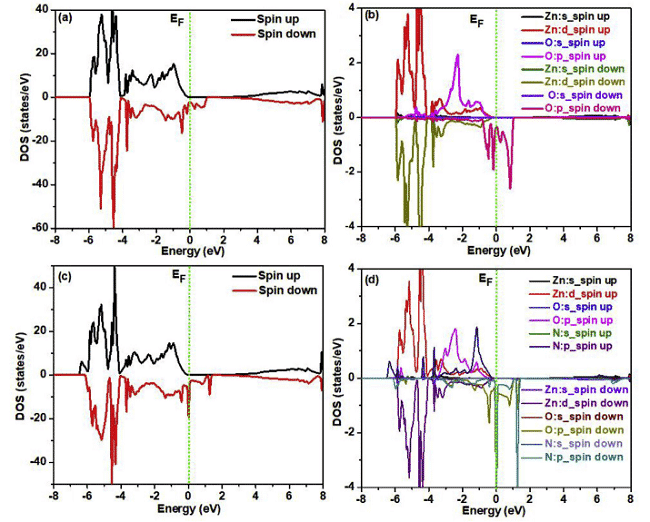
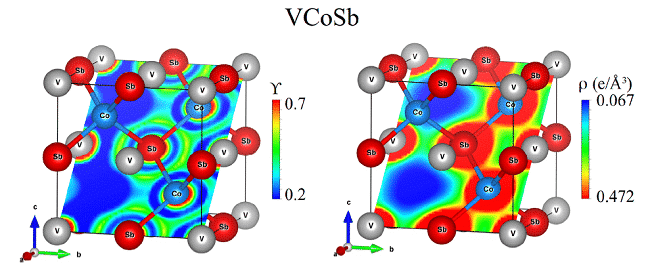
Fig. 5 Distribution de la fonction de localisation des électrons (Y) et de la densité de charge (r) dans le tellurure VCoSb J. Ibá?ez, T. Wo?niak et al. ont testé la validité de différentes théories fonctionnelles de densité pour prédire la dynamique de réseau de HfS2 sous pression.

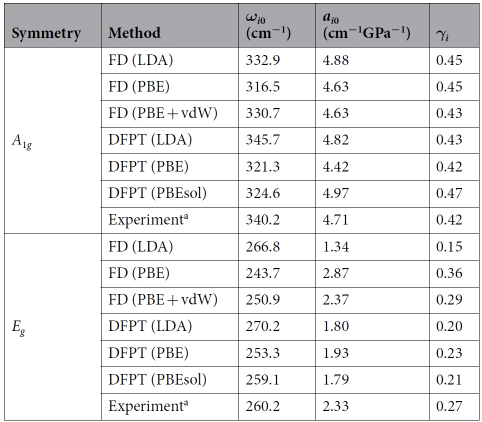
Le tableau d'observation 2 a révélé que GGA-DFT décrit correctement la dynamique du réseau à haute pression de HfS2 en tenant compte de l'interaction vdW, tandis que le calcul LDA-DFT est largement utilisé pour prédire la structure et les caractéristiques de vibration des composés 2D dans des conditions environnementales et ne peut pas être reproduit sous compression. les conditions. Le comportement de HfS2, qui indique que l'utilisation de DFT-LDA pour calculer la compressibilité des TMDC et les paramètres de Grüneisen produira de grandes erreurs [8].

Tableau 2 Fréquence Raman (ωi0), coefficient de pression (ai0) et paramètre de Grüneisen (γi)

En plus des algorithmes LDA et GGA, il existe également des fonctionnelles de densité hybrides qui intègrent les effets d'échange Hatree-Fock (HF) dans les associations d'échange de manière hybride, comme B3LYP, qui était populaire en 1998. Ces théories contiennent de plus en plus informations systématiques, et les résultats de calcul se rapprochent de plus en plus des données expérimentales, particulièrement adaptées au domaine de la chimie organique, et ont obtenu un grand succès dans le calcul du mécanisme de réaction chimique.

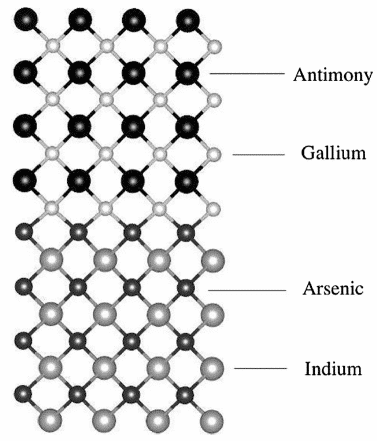
Par exemple, T. Garwood et al. ont calculé les données de bande interdite de la structure de super-réseau de type InAs/GaSb II (modèle illustré à la figure 6) en utilisant l'hybridation de type PBE0 [9], qui est très proche de la valeur expérimentale, et la plage de déviation est d'environ 3 %-11%.

Figure 6 Modèle Ball-and-stick InAs / GaSb SLS de DFT hybride calculé à l'aide de VESTA

La théorie de la structure des bandes d'électrons basée sur le spectre d'énergie d'une seule particule de Kohn-Sham peut décrire qualitativement de nombreux matériaux, mais elle n'est pas satisfaisante d'un point de vue quantitatif. Par exemple, pour des matériaux semi-conducteurs simples tels que Si et GaAs, la bande interdite donnée par le Kohn-Sham DFT sous LDA/GG est beaucoup plus petite ; pour les semi-conducteurs à petite bande interdite tels que Ge et InN, le métal obtenu à partir de LDA/GGA est du métal. état, mais l'observation expérimentale est semi-conducteur, qui est le soi-disant problème de bande interdite LDA / GGA.

Afin de surmonter le problème de la bande interdite, les gens ont fait beaucoup d'efforts dans le cadre théorique de la DFT, comme l'extension de la théorie de Kohn-Sham basée sur le potentiel effectif local à la théorie généralisée de Kohn-Sham (GKS) basée sur la non- potentiel effectif local et autre théorie fonctionnelle de la densité hybride, il existe une théorie des perturbations à plusieurs corps basée sur la fonction de Green à un corps. Dans cette théorie, le potentiel lié à l'échange avec le DFT de Kohn-Sham correspond à l'opérateur d'auto-énergie associé à l'échange. Pour l'opérateur d'auto-énergie, une approximation relativement simple et précise est l'approximation GW (le produit de la fonction de Green à une seule particule G et de l'effet de Coulomb blindé W). En calculant l'opérateur d'auto-énergie sous une certaine approximation, nous pouvons obtenir le PES correspondant (IPS). Les quasi-particules dans l'énergie d'excitation. Bien que ces nouvelles directions de développement aient amélioré la description de la bande interdite des matériaux, les fonctionnelles approchées ont encore une grande subjectivité, et le champ d'application est relativement limité. Jusqu'à présent, il n'existe pas de méthode DFT universelle avec une base théorique suffisante. Une description précise de la structure de bande électronique du matériau [10,11].

De plus, il existe des extensions basées sur la théorie fonctionnelle de la densité existante. Par exemple, la théorie fonctionnelle de la densité dépendante du temps (TDDFT) basée sur la différence d'énergie orbitale KS est utilisée pour remplacer l'équation de Schordinger par l'équation de Dirac à une seule particule. La théorie fonctionnelle de la densité de densité s'étend à LDA + U des systèmes de corrélation forte et à la théorie fonctionnelle de la densité de flux (CDFT) pour traiter les systèmes d'électrons en interaction sous des champs magnétiques arbitraires.

Références

Xiang-Yuan Cui, Simon P. Ringer，Sur le lien entre la microscopie à sonde atomique et les simulations de la théorie fonctionnelle de la densité [J] ，Matériaux

Caractérisation (2018), https://doi.org/10.1016/matchar.2018.05.015

B. Obot, DD Macdonald, ZM Gasem，Théorie fonctionnelle de la densité

(DFT) comme un outil puissant pour concevoir de nouveaux inhibiteurs de corrosion organiques. Partie 1 : Un aper?u [J]，Corrosion Science 99 (2015) 1–30

Geerlings, F. De Proft, W. Langenaeker, théorie fonctionnelle de la densité conceptuelle, Chem. Rév.103 (2003) 1793–1873.

Nagy, Théorie fonctionnelle de la densité et application aux atomes et aux molécules, Rev. 298 (1998) 1–79.

Koch, MC Holthausen, Guide du chimiste sur la théorie fonctionnelle de la densité, Wiley-VCH, Weinheim, 2000.

Asad Mahmood, Fatih Tezcan, Gulfeza Kardas，Décomposition thermique du gel précurseur de Zn0.8Ga0.2O dérivé du sol-gel?: études acinétiques, thermodynamiques et DFT [J]，Acta Materialia 146 (2018) 152-159

Parmod Kumar, Hitendra K. Malik, Anima Ghosh, R. Thangavel, K. Asokan，Un aper?u de l'origine du ferromagnétisme dans ZnO et N

films ZnOthin implantés : Approche expérimentale et DFT [J]，Journal of Alloys and Compounds 768 (2018) 323-328

Romaka, VV Romaka, N. Melnychenko, Yu. Stadnyk, L. Bohun, A. Horyn，étude expérimentale et DFT du système ternaire VeCoeSb[J] ，Journal of Alloys and Compounds 739 (2018) 771-779

Ibá?ez, T. Wo?niak, F. Dybala, R. Oliva, S. Hernández，R. Kudrawiec，Diffusion Raman à haute pression dans le HfS2?: comparaison des méthodes de la théorie de la fonction de la densité dans les composés MS2 en couches (M = Hf, Mo) sous compression [J]，Rapports scientifiques (2018) 8:12757，DOI?: 10.1038/ s41598-018- 31051-y

Garwood, NA Modine, S. Krishna ， Modélisation de la structure électronique des super-réseaux InAs / GaSb avec la théorie fonctionnelle de la densité hybride [J] ， Infrared Physics & Technology 81 (2017) 27–31

Eugene S. Kryachko, Eduardo V. Ludena ， Théorie fonctionnelle de la densité: Fondements examinés [J] ， Physics Reports 544 (2014) 123–239

B. Obot, DD Macdonald, ZM Gasem，Théorie fonctionnelle de la densité (DFT) en tant qu'outil puissant pour la conception de nouveaux inhibiteurs de corrosion organiques. Partie 1 : Un aper?u [J]，Corrosion Science 99 (2015) 1–30