Las grietas por fatiga son generalmente el resultado de deformaciones plásticas periódicas en áreas locales. La fatiga se define como "falla bajo carga repetida u otros tipos de condiciones de carga, y este nivel de carga no es suficiente para causar falla cuando se aplica solo una vez". Esta deformación plástica no se produce por la tensión teórica sobre el componente ideal, sino porque la superficie del componente no se puede detectar realmente.
August W?hler es el pionero de la investigación de la fatiga y propone un método empírico. Entre 1852 y 1870, W?hler estudió el deterioro progresivo de los ejes ferroviarios. él construyó el banco de pruebas que se muestra en la Figura 1. Este banco de pruebas permite girar y doblar dos ejes de ferrocarril al mismo tiempo. W?hler trazó la relación entre la tensión nominal y el número de ciclos que conducen a la falla, lo que más tarde se conoce como diagrama SN. Cada curva sigue llamándose línea de w ? hler. El método Sn sigue siendo el método más utilizado en la actualidad. Un ejemplo típico de esta curva se muestra en la Figura 1.
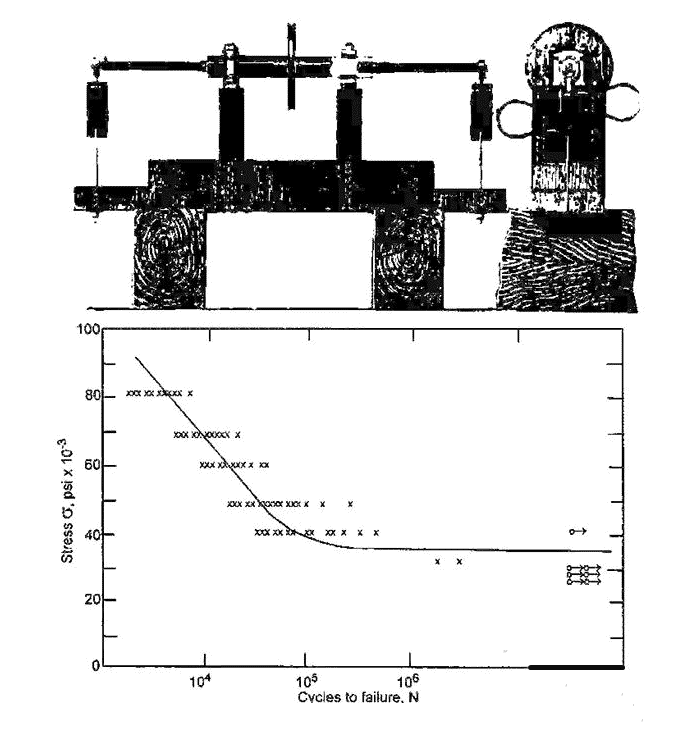
Se pueden observar varios efectos a través de la línea de w?hler. Primero, observamos que la curva SN por debajo del punto de transición (alrededor de 1000 ciclos) no es válida porque el esfuerzo nominal aquí es elastoplástico. Más adelante mostraremos que la fatiga es causada por la liberación de energía de deformación plástica cortante. Por lo tanto, no existe una relación lineal entre la tensión y la deformación antes de la fractura y no se puede utilizar. Entre el punto de transición y el límite de fatiga (alrededor de 107 ciclos), el análisis basado en Sn es válido. Por encima del límite de fatiga, la pendiente de la curva disminuye bruscamente, por lo que esta región a menudo se denomina región de "vida infinita". Pero este no es el caso. Por ejemplo, la aleación de aluminio no tendrá una vida infinita, e incluso el acero no tendrá una vida infinita bajo una carga de amplitud variable.
Con la aparición de la tecnología de amplificación moderna, las personas pueden estudiar las grietas por fatiga con más detalle. Ahora sabemos que la aparición y propagación de grietas por fatiga se puede dividir en dos etapas. En la etapa inicial, la grieta se propaga en un ángulo de unos 45 grados con respecto a la carga aplicada (a lo largo de la línea de esfuerzo cortante máximo). Después de cruzar dos o tres límites de grano, su dirección cambia y se extiende a lo largo de la dirección de unos 90 grados con respecto a la carga aplicada. Estas dos etapas se denominan grieta de etapa I y grieta de etapa II, como se muestra en la Figura 2.
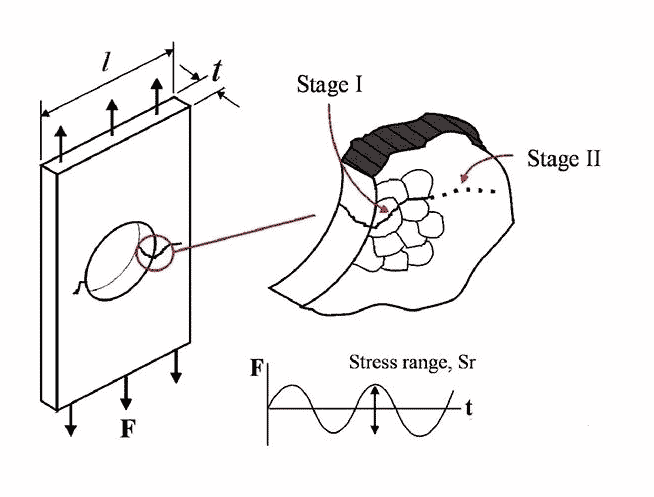
Si observamos una fisura de etapa I a gran aumento, podemos ver que la tensión alterna conducirá a la formación de una banda de deslizamiento continua a lo largo del plano de corte máximo. Estas bandas deslizantes se deslizan hacia adelante y hacia atrás, como una baraja de cartas, lo que da como resultado superficies irregulares. La superficie cóncava finalmente forma una grieta de "brote", como se muestra en la Figura 3. En la fase I, la grieta se expandirá de este modo hasta que alcance el límite de grano y se detendrá temporalmente. Cuando se aplica suficiente energía a los cristales adyacentes, el proceso continúa.
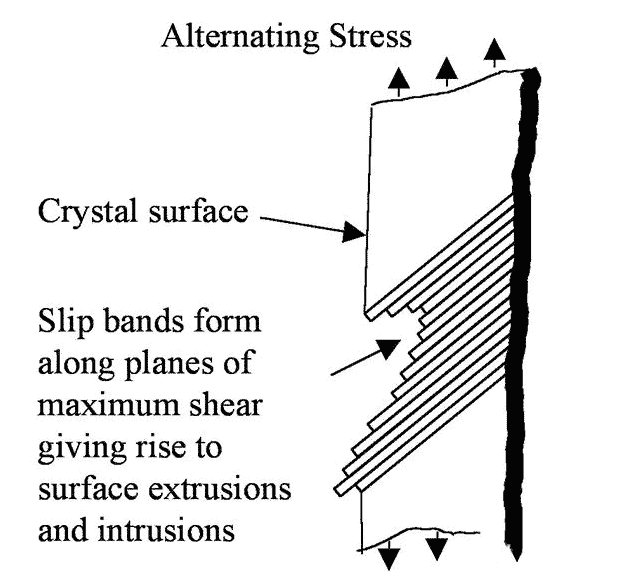
Después de cruzar dos o tres límites de grano, la dirección de propagación de grietas ahora entra en el modo de fase II. En esta etapa, las propiedades físicas de la propagación de grietas han cambiado. La fisura en sí misma constituye un macroobstáculo para el flujo de tensiones, provocando una alta concentración de tensiones plásticas en la punta de la fisura. Como se muestra en la Figura 4. Cabe se?alar que no todas las grietas de la etapa I se desarrollarán a la etapa II.
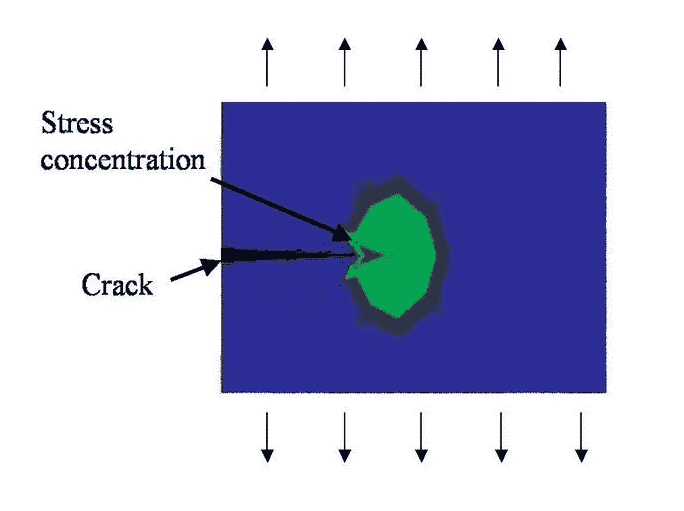
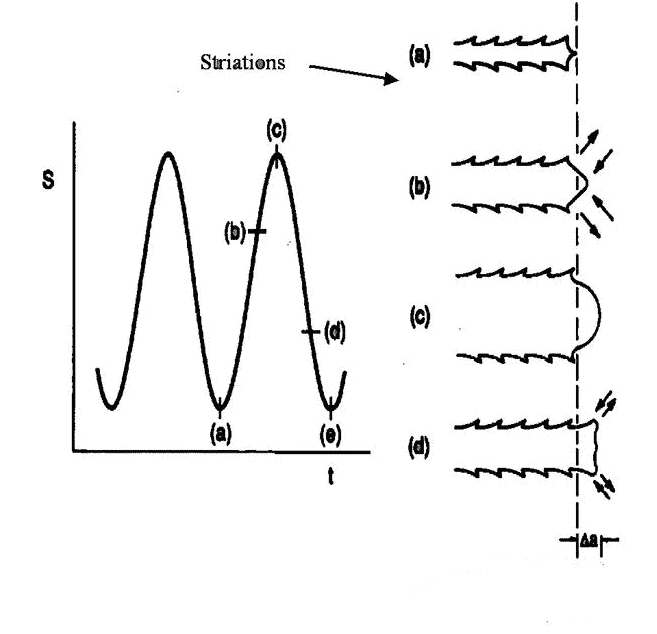
Para comprender el mecanismo de propagación de la etapa II, debemos considerar la situación de la sección transversal de la punta de la grieta durante el ciclo de tensión. Como se muestra en la Figura 5. El ciclo de fatiga comienza cuando el esfuerzo nominal está en el punto “a”. A medida que la intensidad de la tensión aumenta y pasa por el punto "B", notamos que la punta de la fisura se abre, lo que da como resultado una deformación por cortante plástico local, y la fisura se extiende hasta el punto "C" en el metal original. Cuando el esfuerzo de tracción disminuye por el punto “d”, observamos que la punta de la fisura se cierra, pero la deformación plástica permanente deja un único dentado, la llamada “l(fā)ínea de corte”. Cuando todo el ciclo termina en el punto "e", observamos que la fisura ahora ha aumentado la longitud "Da" y ha formado líneas de sección adicionales. Ahora se entiende que el rango de crecimiento de la fisura es proporcional al rango de deformación elástica-plástica aplicada en la punta de la fisura. Un rango de ciclo más grande puede formar un Da más grande.
Factores que afectan la tasa de crecimiento de grietas por fatiga
Se estudia y explica conceptualmente la influencia de los siguientes parámetros en la tasa de crecimiento de grietas por fatiga:
1Esfuerzo cortante
En el diagrama, podemos ver que una cierta "cantidad" de esfuerzo cortante se libera durante el cambio periódico de la resistencia del esfuerzo nominal. Y cuanto mayor sea el rango de cambios de estrés, mayor será la energía liberada. A través de la curva SN que se muestra en la Figura 1, podemos ver que la vida a fatiga disminuye exponencialmente con el aumento del rango del ciclo de estrés.
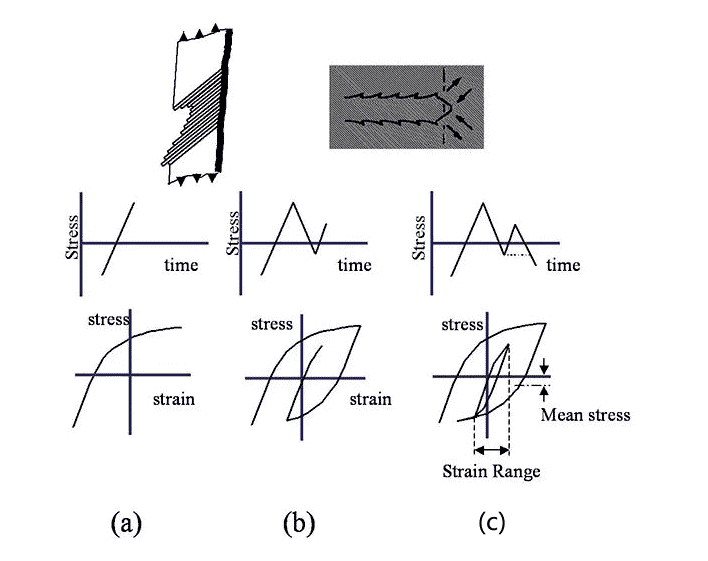
2 tensión media
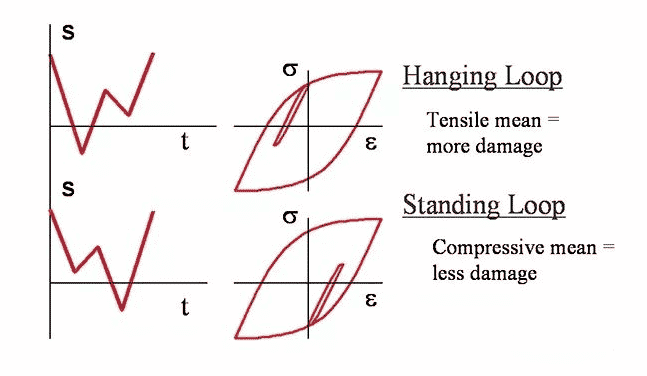
El estrés promedio (esfuerzo residual) también es un factor que afecta la tasa de falla por fatiga. Conceptualmente, si la tensión de expansión se aplica a la fisura de fase II, la fisura se verá forzada a abrirse, por lo que cualquier ciclo de tensión tendrá un efecto más significativo. Por el contrario, si se aplica el esfuerzo de compresión promedio, la fisura se verá forzada a cerrarse y cualquier ciclo de tensión debe superar el esfuerzo de precompresión antes de que la fisura pueda continuar expandiéndose. Conceptos similares también se aplican a las grietas de etapa I.
3 acabado superficial
Debido a que las grietas por fatiga generalmente aparecen primero en la superficie de los componentes donde hay defectos, la calidad de la superficie afectará seriamente la probabilidad de que ocurran grietas. Aunque la mayoría de las muestras de prueba de materiales tienen un acabado de espejo, también lograrán la mejor vida útil a la fatiga. De hecho, la mayoría de los componentes no se pueden comparar con las muestras, por lo que debemos modificar las propiedades de fatiga. El acabado superficial tiene un mayor efecto sobre la fatiga de los componentes sometidos a ciclos de tensión de baja amplitud.
4 tratamiento de superficie
El tratamiento de superficie se puede utilizar para mejorar la resistencia a la fatiga de los componentes. El propósito del tratamiento superficial es formar esfuerzos de compresión residuales en la superficie. Bajo el período de baja amplitud, la tensión en la superficie es obviamente baja e incluso mantiene el estado de compresión. Por lo tanto, la vida de fatiga puede prolongarse significativamente. Sin embargo, como se?alamos, esta situación solo es válida para componentes sujetos a ciclos de tensión de baja amplitud. Si se aplica un período de amplitud alta, la compresión previa será superada por el período de amplitud alta y se perderán sus ventajas. Al igual que con la calidad de la superficie, el impacto del tratamiento de la superficie se puede mostrar mediante modelos.









