To know Young’s modulus well and answer this question on title bar, we need to think about how materials?get elasticity.

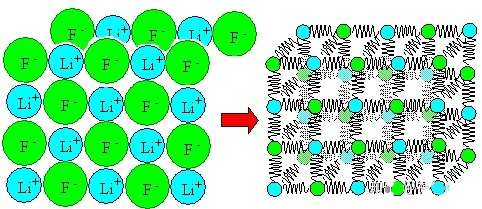
For metal materials, we know that their interior is composed of atoms, many atoms are arranged regularly to form crystals, and many grains are combined together to form the metal we usually see.

Does elasticity come from the interaction between grains? Obviously not, because both single crystal and amorphous have elasticity.

Thus, elasticity probably comes from the interaction between atoms.

In order to be as simple and convenient as possible, we try not to introduce complex concepts or mathematical formulas.?Let’s start with the?simplest diatomic model.

Diatomic model of Young’s modulus

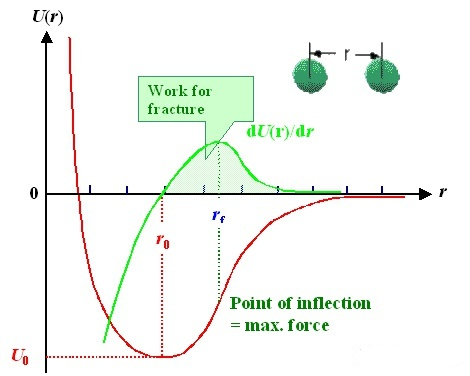
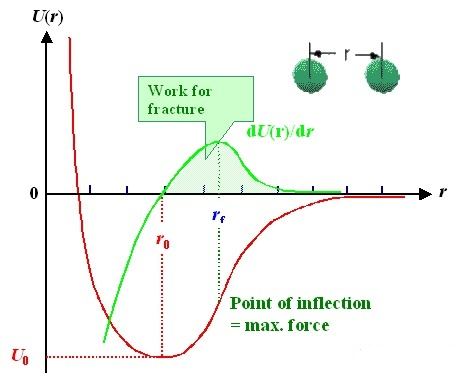
Diatomic model: the interaction between two atoms can be described by potential function (red line). The horizontal axis is the distance“r” between two atoms, and the vertical axis is the potential energy U (r); The interaction force (green line) can be obtained by deriving the potential function. It is worth noting that there is an equilibrium position r0r_ {0} between the two atoms, where the interaction force F = 0 and the potential energy is the lowest; In other words, when you leave this position.No matter to the left or to the right, there will be a force trying to pull it back.

Like a spring, there is such a balance position in the natural state. No matter whether you are squeezing the spring or stretching it, which still rebounds to the original position after releasing your hand.

This is the source of elasticity from the atomic level!

Of course, actual metals or other materials have many atoms inside. These atomic interactions can be simply understood as the superposition of a pair of atomic interactions.

analysis of the relationship between Young’s modulus and other parameters

In general, we can simply assume that this potential function has the following form:

The above function has four variable parameters,which are the equilibrium position R0R_{0}, Biding energy U0U_{0},and parameters N and M. The above parameters may vary for different kinds of Atoms.

Now we take these two atoms as an independent system and stretch or compress them.

In order to change the distance between two atoms near the equilibrium position, the force F to be applied

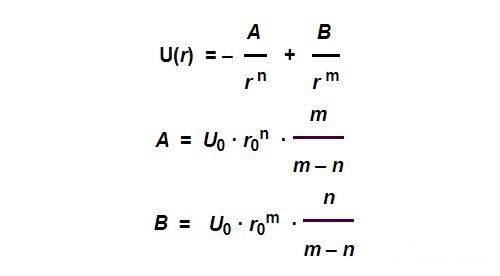
In order to correspond to Young’s modulus, we need to change it into σ= E ε Form, divide by one r02r on both sides_ {0} ^ {2} and substituting the above formula and pretend to operate:

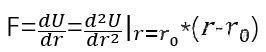
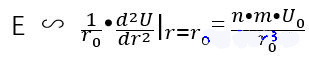
Fazit

That is?to say, Young’s modulus E is mainly affected by N, m, u0u_ {0}、r0r_ {0}. The atomic species and temperature can affect these parameters. The influence of different atomic species is obvious, and all parameters will change. The effect of temperature seems less obvious.

To observe the effect of temperature, we have to go back to the potential function curve itself. Because the potential function is not a perfect symmetric curve, when the temperature rises, it means that the atom moves more vigorously and the range of motion becomes larger, such as thermal expansion and cold contraction. At this time, the balance position r0r_ {0} will be offset, as shown by the green line in the following figure.

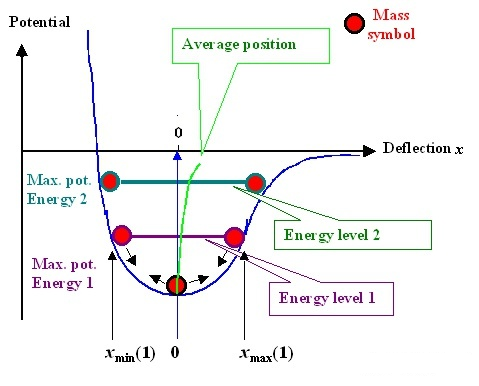
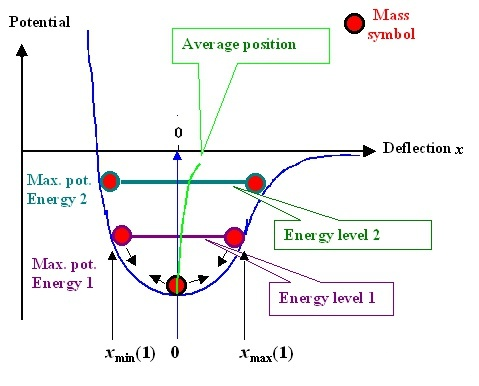
It can be proved that atoms are always in motion. When the temperature is high, the equilibrium position r0r_ The larger {0}, the volume of the material increases and the young’s modulus decreases.

Back to our initial question, the number of iron atoms in different grades of steel can account for more than 90%. Even compared with pure iron, the interaction force between atoms does not change greatly, so its young’s modulus is hardly affected by the change of alloy composition; Similarly, no matter the microstructure changes or work hardening, the rearrangement of atoms does not change the force between atoms, so they do not affect young’s modulus.

In addition to Young’s modulus, physical quantities such as melting point, coefficient of thermal expansion and tensile strength of perfect crystal can also be derived from this model.

As for the abnormal phenomenon that the young’s modulus of rubber in high elastic state increases with the increase of temperature, it is because the source of rubber elasticity is different from that of conventional materials.