Die Dichtefunktionaltheorie (DFT) wurde in den Bereichen der Physik der kondensierten Materie, der Materialwissenschaften, der Quantenchemie und der Biowissenschaften als N?herungsverfahren für den Umgang mit Mehrteilchensystemen weit verbreitet. Beispielsweise ist Abbildung 1(c) eine Superzellenstruktur mit 72 Atomen, die unter Verwendung der DFT-Methode [1] berechnet wurde. Die DFT-basierte materialwissenschaftliche Computersimulationsmethode kann nicht nur vorhandene Materialien untersuchen, sondern auch neue Materialien vorhersagen.

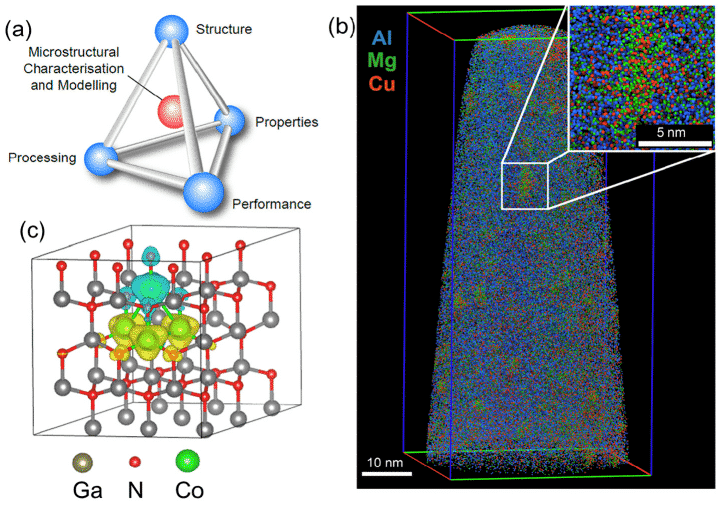
Abbildung 1 (a) M?gliche Verbindung zwischen mikroskopischer Charakterisierung, Struktur, Verarbeitung, Eigenschaften und Eigenschaften, (b) APT-Daten für Al-Cu-Mg-Legierungen mit etwa 20 Millionen Atomen, (c) 72-Atom für DFT-Berechnungen Supercell-Beispiel

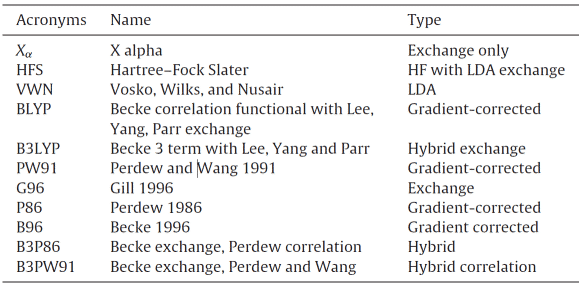
Ein Funktional ist eine Abbildung vom Vektorraum zum Skalar, einer Funktion einer Funktion. Tabelle 1 listet einige der vorgeschlagenen Arten von Dichtefunktionalen auf, von denen einige aus der grundlegenden Quantenmechanik und andere aus parametrischen Funktionen abgeleitet sind, jede mit ihren eigenen Vor- und Nachteilen und ihrem Anwendungsbereich [2]. Das Wesen der DFT-Methode besteht darin, die Elektronendichte als Tr?ger aller Informationen im molekularen (atomaren) Grundzustand zu verwenden und nicht die Wellenfunktion eines einzelnen Elektrons, so dass das Mehrelektronensystem in ein umgewandelt werden kann Einzelelektronenproblem. Unter der Annahme, dass die Anzahl der Elektronen N ist, betr?gt die Anzahl der Variablen in der Wellenfunktion 3 N, und die Dichtefunktionaltheorie reduziert die Anzahl der Variablen auf drei r?umliche Variablen, was den Berechnungsprozess vereinfacht und die Berechnungsgenauigkeit sicherstellt.

Tabelle 1 Einige ungef?hre Dichtefunktionaltypen

Die Entwicklung der Dichtefunktionaltheorie l?sst sich grob in drei Phasen einteilen. Die erste Phase war 1927. Thomas und Fermi schlugen das Thomas-Fermi-Modell vor, das auf der Hypothese des idealen elektronischen Gases unter idealen Bedingungen basiert. Erstmals wurde das Konzept der Dichtefunktionaltheorie eingeführt, das zum Prototyp des sp?teren DFT-Verfahrens wurde.

Der Ausgangspunkt des Thomas-Fermi-Modells ist die Annahme, dass es keine Wechselwirkung zwischen Elektronen und keine ?u?ere St?rung gibt, dann kann die Schr?dinger-Gleichung für die Elektronenbewegung ausgedrückt werden als:

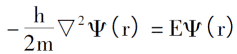
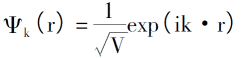
Mit Einführung des Gesetzes der Elektronenanordnung unter 0K sind die Elektronendichte, die Gesamtenergie einzelner Elektronen und die kinetische Energiedichte des Systems:

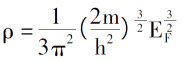
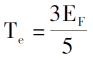
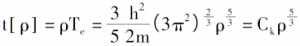
Durch die Einführung einer Beschreibung des Coulomb-Potentials und des externen Feldes zwischen Elektronen kann der Gesamtenergieausdruck des elektronischen Systems, der nur durch die Elektronendichtefunktion bestimmt wird, abgeleitet werden [3].

Obwohl das Modell die Berechnungsform und den Prozess vereinfacht, berücksichtigt es nicht die Wechselwirkung zwischen Elektronen. Es beschreibt die kinetischen Energieelemente nicht genau und ist daher in vielen Systemen nicht anwendbar. Inspiriert von dieser neuartigen Forschungsidee haben die einschl?gigen Wissenschaftler die Dichtefunktionaltheorie jedoch in den 1960er Jahren nach langj?hrigen Bemühungen im Wesentlichen perfektioniert und schlie?lich eine strenge Dichtefunktionaltheorie etabliert.

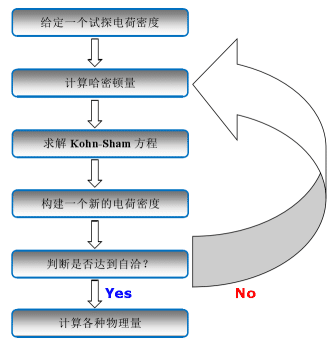
Abbildung 2 Schematische Darstellung eines selbstkonsistenten iterativen Prozesses basierend auf DFT

Das Hohenberg-Kohn-Theorem und die Kohn-Sham-Gleichung haben eine Schlüsselrolle bei der Entwicklung und Verbesserung der DFT-Methode gespielt und wurden als die beiden Eckpfeiler der DFT gefeiert.

(1) Satz von Hohenberg-Kohn

Die Kernidee des Hohenberg-Kohn-Theorems besteht darin, dass alle physikalischen Gr??en im System eindeutig durch Variablen bestimmt werden k?nnen, die nur die Elektronendichte enthalten, und die Implementierungsmethode darin besteht, den Grundzustand des Systems durch das Variationsprinzip zu erhalten. Diese Theorie gilt haupts?chlich für das ungleichm??ige Elektronengasmodell und besteht aus zwei Untertheoremen. i) ein Elektronensystem, das den Spin bei dem externen Potential (einem anderen Potential als der elektronischen Wechselwirkung) ignoriert, dessen externes Potential eindeutig durch die Elektronendichte bestimmt werden kann; ii) für ein gegebenes externes Potential ist die Grundzustandsenergie des Systems das Minimum des Energiefunktionswerts. Somit kann das Energiefunktional des Systems beschrieben werden als:

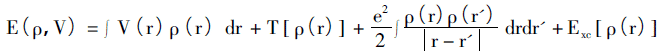
Die rechte Seite der Gleichung ist die potentielle Energie, der Term der kinetischen Energie, die Coulomb-Wechselwirkung zwischen Elektronen und die austauschbezogene potentielle Energie im externen Feld.

Dieser Satz gibt keine spezifischen Ausdrücke für die Elektronendichtefunktion, das kinetische Energiefunktional und das austauschbezogene Funktional an, sodass die spezifische L?sung immer noch nicht m?glich ist.

(2) Kohn-Sham-Gleichung

Bis 1965 stellten Kohn und Shen Lujiu die Kohn-Sham-Gleichung auf und gaben eine detaillierte Beschreibung jedes Elements, und die Dichtefunktionaltheorie begann, in die Phase der praktischen Anwendung einzutreten. Sie schlugen für die Funktionale der kinetischen Energie vor, die Funktionale der kinetischen Energie der Partikel ohne Wechselwirkung zu verwenden, um die Substitution anzun?hern, und die Unterschiede zwischen den beiden sind in den Unbekannten der austauschbezogenen Funktionale enthalten [4]. Die Variation von ρ wird durch die ersetzt Variation von Φi(r), und der Lagrange-Multiplikator wird durch Ei ersetzt. Die Einzelelektronengleichung lautet:

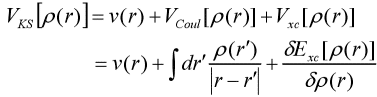
Das Obige ist die Kohn-Sham-Gleichung.

Die Kohn-Sham-Gleichung bringt alles au?erhalb des austauschassoziierten Funktionals klar zum Ausdruck und ordnet auch komplexe Effekte diesem Begriff zu. An dieser Stelle wird die Rechenschwierigkeit stark vereinfacht, und die ganze Arbeit beginnt damit, die austauschbezogene funktionale Erweiterung zu beschreiben. Gleichzeitig bestimmt die ungef?hre Form des austauschbedingten Potentials auch direkt die Genauigkeit der Dichtefunktionaltheorie.

Das Local Density Approximation (LDA)-Verfahren wurde ebenfalls 1965 von Kohn und Shen Lujiu vorgeschlagen. Der Zweck besteht darin, die unbekannten Austauschassoziationen zu approximieren, so dass das DFT-Verfahren für die tats?chliche Berechnung verwendet werden kann. LDA verwendet die Dichtefunktion von einheitlichem Elektronengas, um die Austauschbeziehung von uneinheitlichem Elektronengas zu berechnen. Unter der Annahme, dass sich die Elektronendichte im System mit dem Raum nur sehr wenig ?ndert, kann die Austauschbeziehung von ungleichm??igem Elektronengas ausgedrückt werden als:

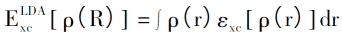
Das entsprechende Austauschkorrelationspotential kann ausgedrückt werden als:

Asad Mahmood et al. verwendeten VASP, um die Gleichgewichtsstrukturparameter von LDA-PBE- und GGA-PAW-Berechnungen zu vergleichen, und untersuchten die Auswirkungen der Ga-Dotierung auf die Elektronenorbital-Hybridisierung sowie die optischen Eigenschaften und die Kristallgeometrie aus Abbildung 3(c). Es ist ersichtlich, dass die Ga-2s- und Ga-2p-Orbitale erheblich zur Leitung beitragen, das niedrigere VB tr?gt auch durch Ga-2p bei, und das Verunreinigungsband am unteren Rand des CB deutet auf eine zus?tzliche Energiebarriere hin, das Elektron zwischen VB und CB. Der übergang muss die Energiebarriere überschreiten [5].

Abbildung 3 Berechnungsergebnisse

(a) Optimierte 3x3x3 Ga-dotierte ZnO-Superzelle, (b) Bandstruktur, (c) Dichte DOS

Um das tats?chliche Materialsystem genauer zu berechnen, haben Becke, Perdew und Wang et al. vorgeschlagene Generalized Gradient Approximation (GGA), die am weitesten verbreitete Verarbeitungsmethode bei der Dichtefunktionalberechnung.

Die GGA-Verarbeitungsmethode besteht darin, die ursprüngliche Darstellung in eine funktionale Form umzuschreiben, die Elektronendichte- und Gradientenfunktionen sowie eine Beschreibung des Spins enth?lt, und die resultierende austauschbezogene Funktion lautet wie folgt:

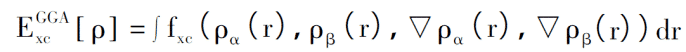
In GGA kann das Austauschkorrelationspotential auch in Austauschenergie und Korrelationsenergie zerlegt werden. Wie konstruieren Sie also einen vernünftigen Ausdruck für diese beiden Teile? Beckc et al. glauben, dass die konkrete Funktionsform prinzipiell beliebig konstruiert werden kann und nicht auf die eigentliche physikalische Bedeutung Rücksicht nehmen muss, wie etwa GGA-PW91; w?hrend Perdew et al. pl?diert dafür, so weit wie m?glich zur reinen quantenmechanischen Rechentheorie zurückzukehren, alle physikalischen Gr??en werden nur berechnet. Ausgehend von grundlegenden Konstanten wie elektrostatischer Masse, Planckscher Konstante und Lichtgeschwindigkeit sollten Funktionsausdrücke keine überm??igen empirischen Parameter enthalten, wie z. B. GGA-PBE (Perdew-Burke-Enzerhoff), das h?ufig in Bereichen wie kondensierter Materie verwendet wird Physik.

Kürzlich haben Parmod Kumar und L. Romaka et al. verwandte Untersuchungen mit FP-LAPW (Full Potential Linearly Enhanced Plane Wave) in WIEN2k bzw. Elk v2.3.22 durchgeführt, bei denen das Austauschkorrelationspotential in Form von GGA-PBE vorliegt, Abbildung 4, 5 Berechnete Ergebnisse für die entsprechenden Zustandsdichte und Ladungsdichteverteilung [6,7].

Abb. 4 Gesamtzustandsdichte und lokale Zustandsdichte spinpolarisierter ZnO-Superzellen ohne N-Injektion und -Implantation

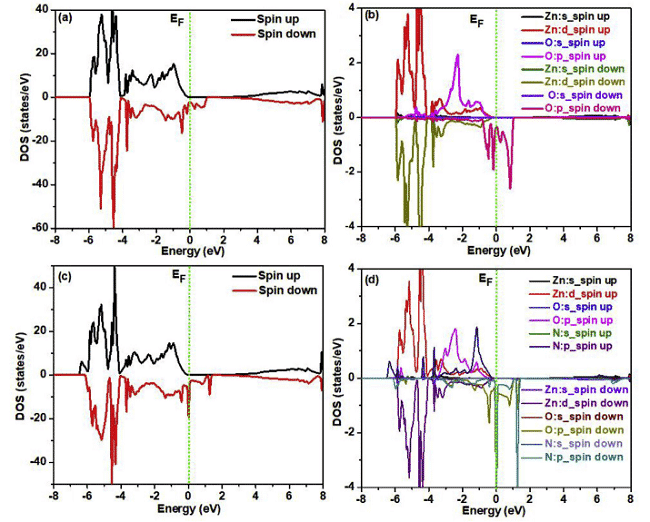
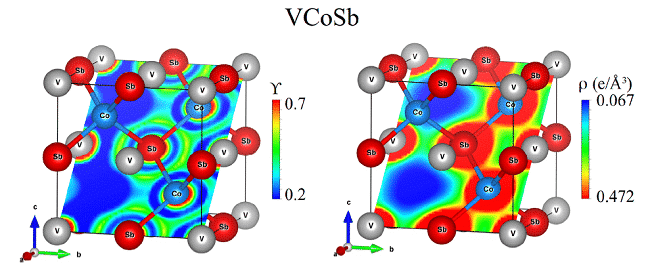
Abb. 5 Verteilung der Elektronenlokalisierungsfunktion (Y) und Ladungsdichte (r) in VCoSb-Tellurid J. Ibá?ez, T. Wo?niak et al. testeten die Gültigkeit der Theorie unterschiedlicher Dichtefunktionen zur Vorhersage der Gitterdynamik von HfS2 unter Druck.

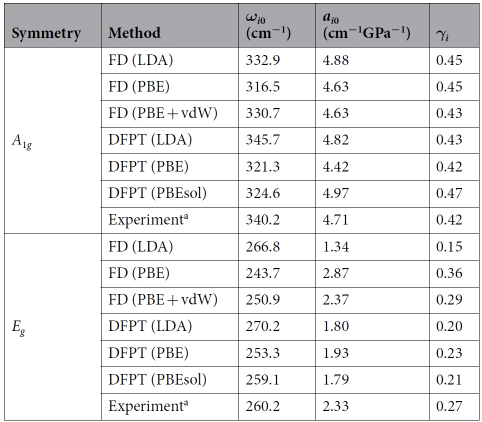
Beobachtungstabelle 2 ergab, dass GGA-DFT die Hochdruck-Gitterdynamik von HfS2 unter Berücksichtigung der vdW-Wechselwirkung richtig beschreibt, w?hrend die LDA-DFT-Berechnung weit verbreitet ist, um die Struktur und Schwingungseigenschaften von 2D-Verbindungen unter Umgebungsbedingungen vorherzusagen, und unter Kompression nicht reproduziert werden kann Bedingungen. Das Verhalten von HfS2, das darauf hinweist, dass die Verwendung von DFT-LDA zur Berechnung der Kompressibilit?t der TMDCs und der Grüneisen-Parameter gro?e Fehler erzeugen wird [8].

Tabelle 2 Raman-Frequenz (ωi0), Druckkoeffizient (ai0) und Grüneisen-Parameter (γi)

Neben den LDA- und GGA-Algorithmen gibt es auch hybride Dichtefunktionale, die Hatree-Fock (HF)-Austauscheffekte auf hybride Weise in die Austauschassoziationen einbauen, wie z. B. das 1998 popul?re B3LYP. Diese Theorien beinhalten immer mehr systematische Informationen, und die Berechnungsergebnisse kommen den experimentellen Daten immer n?her, besonders geeignet für das Gebiet der organischen Chemie, und haben gro?e Erfolge bei der Berechnung chemischer Reaktionsmechanismen erzielt.

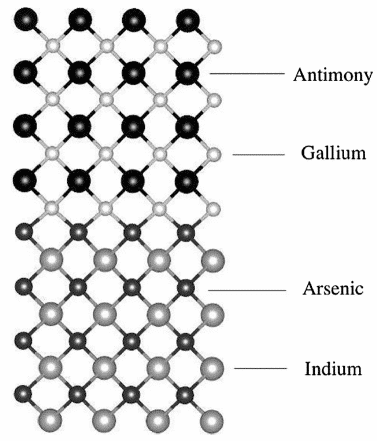
T. Garwood et al. berechneten die Bandlückendaten der übergitterstruktur vom InAs/GaSb II-Typ (Modell in Abbildung 6) unter Verwendung der PBE0-Typ-Hybridisierung [9], die dem experimentellen Wert sehr nahe kommt, und der Abweichungsbereich betr?gt etwa 3 %-11%.

Abbildung 6 Ball-and-Stick-InAs/GaSb-SLS-Modell einer hybriden DFT, berechnet mit VESTA

Die auf dem Kohn-Sham-Einzelteilchen-Energiespektrum basierende Elektronenbandstrukturtheorie kann viele Materialien qualitativ beschreiben, ist jedoch aus quantitativer Sicht nicht zufriedenstellend. Beispielsweise ist für einfache Halbleitermaterialien wie Si und GaAs die durch die Kohn-Sham-DFT unter LDA/GG angegebene Bandlücke viel kleiner; für Halbleiter mit kleiner Bandlücke wie Ge und InN ist das aus LDA/GGA erhaltene Metall Metall. Zustand, aber die experimentelle Beobachtung ist Halbleiter, das ist das sogenannte LDA / GGA-Bandlückenproblem.

Um das Problem der Bandlücke zu überwinden, wurden viele Anstrengungen im theoretischen Rahmen der DFT unternommen, wie z. lokales effektives Potential und andere hybride Dichtefunktionaltheorie, es gibt eine Mehrk?rper-St?rungstheorie, die auf der Eink?rper-Green-Funktion basiert. In dieser Theorie entspricht das austauschbezogene Potential mit der Kohn-Sham DFT dem austauschassoziierten Selbstenergieoperator. Eine relativ einfache und genaue N?herung für den Selbstenergieoperator ist die GW-N?herung (das Produkt der Einzelteilchen-Green-Funktion G und des abgeschirmten Coulomb-Effekts W). Durch Berechnung des Selbstenergieoperators unter einer bestimmten N?herung k?nnen wir die entsprechende PES (IPS) erhalten. Die Quasiteilchen in der Anregungsenergie. Obwohl diese neuen Entwicklungsrichtungen die Beschreibung der Bandlücke von Materialien verbessert haben, haben die ungef?hren Funktionale immer noch eine gro?e Subjektivit?t und der Anwendungsbereich ist relativ begrenzt. Bisher gibt es kein universelles DFT-Verfahren mit ausreichender theoretischer Grundlage. Eine genaue Beschreibung der elektronischen Bandstruktur des Materials [10,11].

Darüber hinaus gibt es einige Erweiterungen, die auf der bestehenden Dichtefunktionaltheorie basieren. Zum Beispiel wird die zeitabh?ngige Dichtefunktionaltheorie (TDDFT) basierend auf der KS-Orbitalenergiedifferenz verwendet, um die Schordinger-Gleichung durch die Einzelteilchen-Dirac-Gleichung zu ersetzen. Die Dichtefunktionaltheorie erstreckt sich auf LDA+U von starken Korrelationssystemen und die Flussdichtefunktionaltheorie (CDFT) für den Umgang mit wechselwirkenden Elektronensystemen unter beliebigen Magnetfeldern.

Verweise

Xiang-Yuan Cui, Simon P. Ringer，über die Verbindung zwischen Atomsondenmikroskopie und Simulationen der Dichtefunktionaltheorie [J] ，Materialien

Charakterisierung (2018), https://doi.org/10.1016/matchar.2018.05.015

B. Obot, DD Macdonald, ZM Gasem, Dichtefunktionaltheorie

(DFT) als leistungsf?higes Werkzeug für die Entwicklung neuer organischer Korrosionsinhibitoren. Teil 1: Ein überblick [J]，Corrosion Science 99 (2015) 1–30

Geerlings, F. De Proft, W. Langenaeker, Konzeptionelle Dichtefunktionaltheorie,Chem. Rev. 103 (2003) 1793–1873.

Nagy, Dichtefunktionaltheorie und Anwendung auf Atome und Moleküle, Rev. 298 (1998) 1–79.

Koch, MC Holthausen, A Chemist's Guide to Density Functional Theory, Wiley-VCH, Weinheim, 2000.

Asad Mahmood, Fatih Tezcan, Gulfeza Kardas, Thermische Zersetzung von Sol-Gel abgeleitetem Zn0,8Ga0,2O-Vorl?ufergel: Akinetic, thermodynamic, and DFT studies [J], Acta Materialia 146 (2018) 152-159

Parmod Kumar, Hitendra K. Malik, Anima Ghosh, R. Thangavel, K. Asokan, Ein Einblick in den Ursprung des Ferromagnetismus in ZnO und N

implantierte ZnOthin-Filme: Experimental and DFT approach [J], Journal of Alloys and Compounds 768 (2018) 323-328

Romaka, VV Romaka, N. Melnychenko, Yu. Stadnyk, L. Bohun, A. Horyn，Experimental and DFT study of the VeCoeSb ternary system[J] ，Journal of Alloys and Compounds 739 (2018) 771-779

Ibá?ez, T. Wo?niak, F. Dybala, R. Oliva, S. Hernández，R. Kudrawiec，Hochdruck-Ramanstreuung in Masse HfS2: Vergleich von Methoden der Dichtefunktionaltheorie in geschichteten MS2-Verbindungen (M = Hf, Mo) unter Kompression [J]，Wissenschaftliche Berichte (2018) 8:12757，DOI: 10.1038/ s41598-018- 31051-y

Garwood, NA Modine, S. Krishna，Elektronische Strukturmodellierung von InAs/GaSb-übergittern mit hybrider Dichtefunktionaltheorie [J]，Infrared Physics & Technology 81 (2017) 27–31

Eugene S. Kryachko, Eduardo V. Ludena，Dichtefunktionaltheorie: Grundlagen überprüft[J]，Physics Reports 544 (2014) 123–239

B. Obot, DD Macdonald, ZM Gasem，Dichtefunktionaltheorie (DFT) als leistungsf?higes Werkzeug für die Entwicklung neuer organischer Korrosionsinhibitoren. Teil 1: Ein überblick [J]，Corrosion Science 99 (2015) 1–30